
Question Number 121138 by Ar Brandon last updated on 05/Nov/20

Answered by TANMAY PANACEA last updated on 05/Nov/20

$${x}^{{x}−{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} } =\left({x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{{x}+{x}^{\frac{−\mathrm{1}}{\mathrm{2}}} } \\ $$$${x}−{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{−{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{3}{x}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{3}{x}={x}^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{1} \\ $$$${x}^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{3}}\rightarrow{x}=\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} =\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{9}}} \\ $$$${y}=\frac{\mathrm{1}}{\:\sqrt{{x}}}=\frac{\mathrm{1}}{\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}}}=\sqrt[{\left.\right)}]{\mathrm{3}}\: \\ $$$${option}\:{D}\left(\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{9}}},\sqrt[{\mathrm{3}}]{\mathrm{3}}\:\right) \\ $$
Commented by Ar Brandon last updated on 05/Nov/20
Thanks Sir
Commented by TANMAY PANACEA last updated on 05/Nov/20
$${most}\:{welcome}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Nov/20
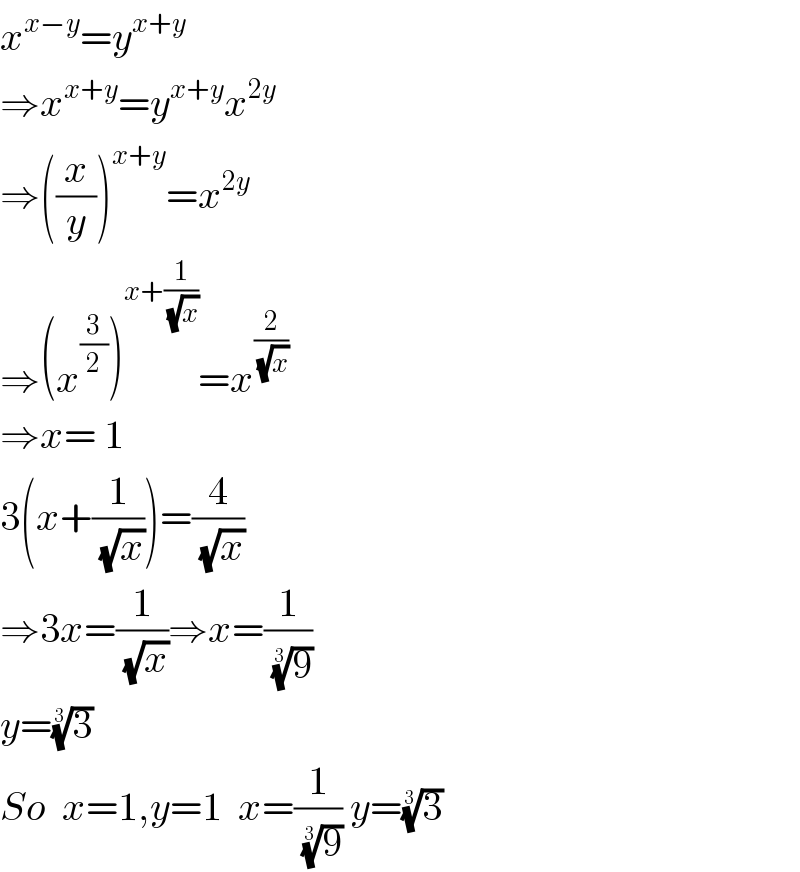
$${x}^{{x}−{y}} ={y}^{{x}+{y}} \\ $$$$\Rightarrow{x}^{{x}+{y}} ={y}^{{x}+{y}} {x}^{\mathrm{2}{y}} \\ $$$$\Rightarrow\left(\frac{{x}}{{y}}\right)^{{x}+{y}} ={x}^{\mathrm{2}{y}} \\ $$$$\Rightarrow\left({x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)^{{x}+\frac{\mathrm{1}}{\:\sqrt{{x}}}} ={x}^{\frac{\mathrm{2}}{\:\sqrt{{x}}}} \\ $$$$\Rightarrow{x}=\:\mathrm{1} \\ $$$$\mathrm{3}\left({x}+\frac{\mathrm{1}}{\:\sqrt{{x}}}\right)=\frac{\mathrm{4}}{\:\sqrt{{x}}} \\ $$$$\Rightarrow\mathrm{3}{x}=\frac{\mathrm{1}}{\:\sqrt{{x}}}\Rightarrow{x}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{9}}} \\ $$$${y}=\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$${So}\:\:{x}=\mathrm{1},{y}=\mathrm{1}\:\:{x}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{9}}}\:{y}=\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$
Commented by Ar Brandon last updated on 05/Nov/20
Brilliant ! Thanks Mr Dwaipayan����
Commented by Ar Brandon last updated on 05/Nov/20
��You'll have to get used-to it bro��
