
Question Number 121099 by Anuragkar last updated on 05/Nov/20
![Let α be a root of x^5 −x^3 +x−2=0 Then prove that [α^6 ]=3 where[λ] denotes greatest integer less than or equal λ](Q121099.png)
$${Let}\:\alpha\:{be}\:{a}\:{root}\:{of}\:\:{x}^{\mathrm{5}} −{x}^{\mathrm{3}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$${Then}\:{prove}\:{that}\:\:\:\left[\alpha^{\mathrm{6}} \right]=\mathrm{3}\:\:\:\:\:\:\:{where}\left[\lambda\right]\:\:{denotes}\:{greatest}\:{integer} \\ $$$${less}\:{than}\:{or}\:\:{equal}\:\lambda \\ $$
Answered by TANMAY PANACEA last updated on 05/Nov/20
![f(x)=x^5 −x^3 +x−2 f(0)<0 f(1)<0 f(2)>0 so root 2>α>1 using graph app ..α=1.206→α^6 ≈3.08 [α^6 ] =[3.08]=3](Q121160.png)
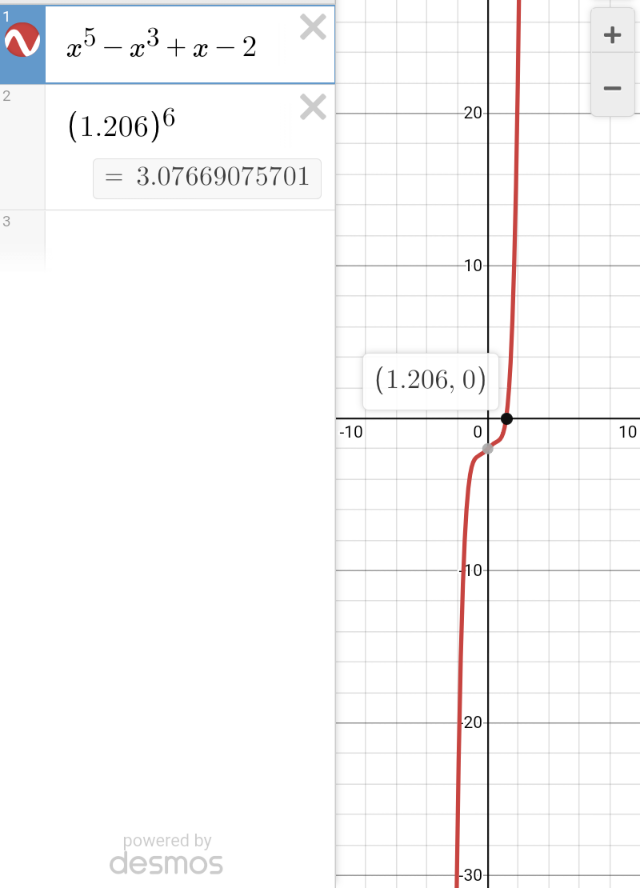
$${f}\left({x}\right)={x}^{\mathrm{5}} −{x}^{\mathrm{3}} +{x}−\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)>\mathrm{0} \\ $$$${so}\:{root}\:\:\:\mathrm{2}>\alpha>\mathrm{1}\: \\ $$$${using}\:{graph}\:{app}\:..\alpha=\mathrm{1}.\mathrm{206}\rightarrow\alpha^{\mathrm{6}} \approx\mathrm{3}.\mathrm{08} \\ $$$$\left[\alpha^{\mathrm{6}} \right] \\ $$$$=\left[\mathrm{3}.\mathrm{08}\right]=\mathrm{3} \\ $$$$ \\ $$
Commented by TANMAY PANACEA last updated on 05/Nov/20
Commented by Anuragkar last updated on 13/Nov/20
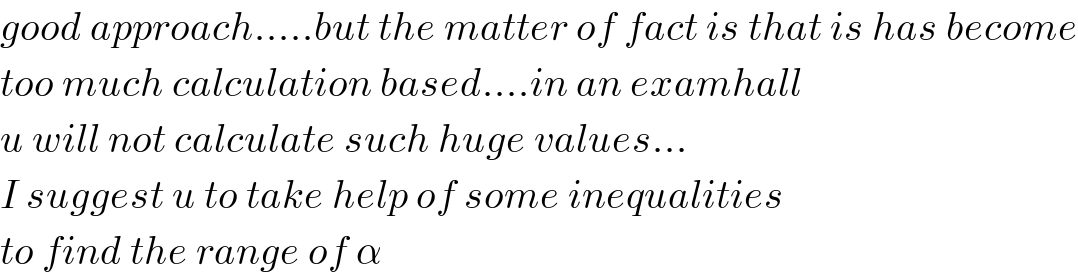
$${good}\:{approach}.....{but}\:{the}\:{matter}\:{of}\:{fact}\:{is}\:{that}\:{is}\:{has}\:{become} \\ $$$${too}\:{much}\:{calculation}\:{based}....{in}\:{an}\:{examhall}\: \\ $$$${u}\:{will}\:{not}\:{calculate}\:{such}\:{huge}\:{values}... \\ $$$${I}\:{suggest}\:{u}\:{to}\:{take}\:{help}\:{of}\:{some}\:{inequalities}\: \\ $$$${to}\:{find}\:{the}\:{range}\:{of}\:\alpha \\ $$
