
Question Number 121029 by bramlexs22 last updated on 05/Nov/20
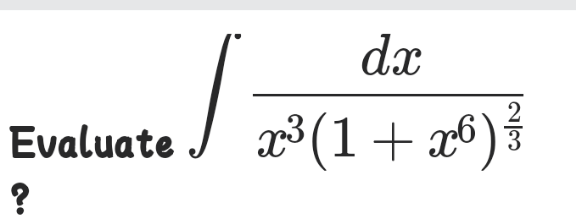
Commented by bobhans last updated on 05/Nov/20

$${super}\:{macho}...! \\ $$
Answered by MJS_new last updated on 05/Nov/20
![super easy lol! ∫(dx/(x^3 (x^6 +1)^(2/3) ))= [t=(((x^6 +1)^(1/3) )/x^2 ) → dx=−((x^3 (x^6 +1)^(2/3) )/2)dt] =−(1/2)∫dt=−(t/2)=−(((x^6 +1)^(1/3) )/(2x^2 ))+C](Q121032.png)
$$\mathrm{super}\:\mathrm{easy}\:\mathrm{lol}! \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{3}} \left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} }{{x}^{\mathrm{2}} }\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{3}} \left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{2}}{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int{dt}=−\frac{{t}}{\mathrm{2}}=−\frac{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} }{\mathrm{2}{x}^{\mathrm{2}} }+{C} \\ $$
Commented by bobhans last updated on 05/Nov/20

$${haha}...{typo}\:{why}\:{denomurator} \\ $$$${x}^{\mathrm{3}} +\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:?\: \\ $$
Commented by MJS_new last updated on 05/Nov/20
![because key [ + ] very close to key [ ( ] on display and typing in jolting bus](Q121036.png)
$$\mathrm{because}\:\mathrm{key}\:\left[\:+\:\right]\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\mathrm{key}\:\left[\:\left(\:\right]\:\mathrm{on}\right. \\ $$$$\mathrm{display}\:\mathrm{and}\:\mathrm{typing}\:\mathrm{in}\:\mathrm{jolting}\:\mathrm{bus} \\ $$
Commented by bramlexs22 last updated on 05/Nov/20
����������
Answered by bobhans last updated on 05/Nov/20
![η = ∫ (dx/(x^3 (x^6 (1+x^(−6) ))^(2/3) )) η = ∫ (dx/(x^7 (1+x^(−6) )^(2/3) )) η = ∫ ((x^(−7) dx )/((1+x^(−6) )^(2/3) )) ; [ t = 1+x^(−6) ] η = −(1/6)∫ (dt/t^(2/3) ) = −(1/6)∫ t^(−2/3) dt η = −(1/2)t^(1/3) + c = −(1/2)((1+x^(−6) ))^(1/3) + c](Q121033.png)
$$\:\eta\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{3}} \left({x}^{\mathrm{6}} \left(\mathrm{1}+{x}^{−\mathrm{6}} \right)\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\eta\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{7}} \left(\mathrm{1}+{x}^{−\mathrm{6}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\eta\:=\:\int\:\frac{{x}^{−\mathrm{7}} \:{dx}\:}{\left(\mathrm{1}+{x}^{−\mathrm{6}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} }\:;\:\left[\:{t}\:=\:\mathrm{1}+{x}^{−\mathrm{6}} \:\right] \\ $$$$\eta\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\int\:\frac{{dt}}{{t}^{\mathrm{2}/\mathrm{3}} }\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\int\:{t}^{−\mathrm{2}/\mathrm{3}} \:{dt} \\ $$$$\eta\:=\:−\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{1}/\mathrm{3}} \:+\:{c}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{1}+{x}^{−\mathrm{6}} }\:+\:{c}\: \\ $$
Commented by MJS_new last updated on 05/Nov/20

$$\mathrm{also}\:\mathrm{very}\:\mathrm{nice}! \\ $$
