
Question Number 120927 by Ar Brandon last updated on 04/Nov/20

Answered by 675480065 last updated on 04/Nov/20

$$\mathrm{domain}:\:\mathrm{2x}−\mathrm{3}/\mathrm{4}\:>\mathrm{0}\:\cap\:\mathrm{x}>\mathrm{0}\:\cap\:\mathrm{x}>\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}>\mathrm{3}/\mathrm{8}\:\cap\:\mathrm{x}>\mathrm{0} \\ $$$$\mathrm{hence}\:\mathrm{2x}−\mathrm{3}/\mathrm{4}\:>\:\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}/\mathrm{4}\:<\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{x}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{Final}\:\mathrm{ans}:\: \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{8}},\:\frac{\mathrm{1}}{\mathrm{2}}\right)\cup\left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{B} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
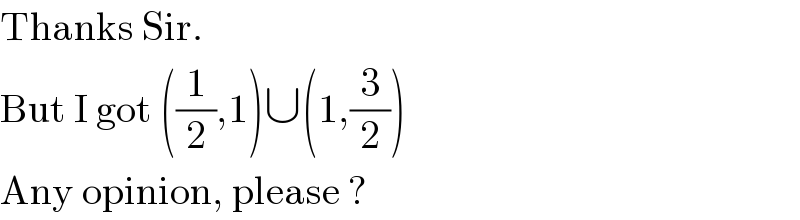
$$\mathrm{Thanks}\:\mathrm{Sir}.\: \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{got}\:\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right)\cup\left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{Any}\:\mathrm{opinion},\:\mathrm{please}\:? \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
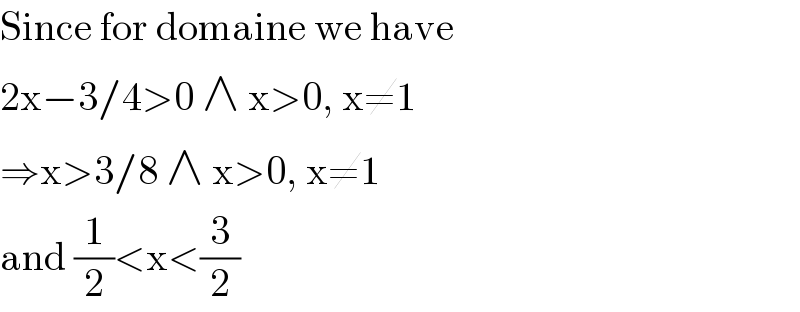
$$\mathrm{Since}\:\mathrm{for}\:\mathrm{domaine}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2x}−\mathrm{3}/\mathrm{4}>\mathrm{0}\:\wedge\:\mathrm{x}>\mathrm{0},\:\mathrm{x}\neq\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}>\mathrm{3}/\mathrm{8}\:\wedge\:\mathrm{x}>\mathrm{0},\:\mathrm{x}\neq\mathrm{1} \\ $$$$\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{x}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by 675480065 last updated on 04/Nov/20

$$\mathrm{this}\:\mathrm{is}\:\mathrm{false} \\ $$$$ \\ $$
Answered by liberty last updated on 04/Nov/20
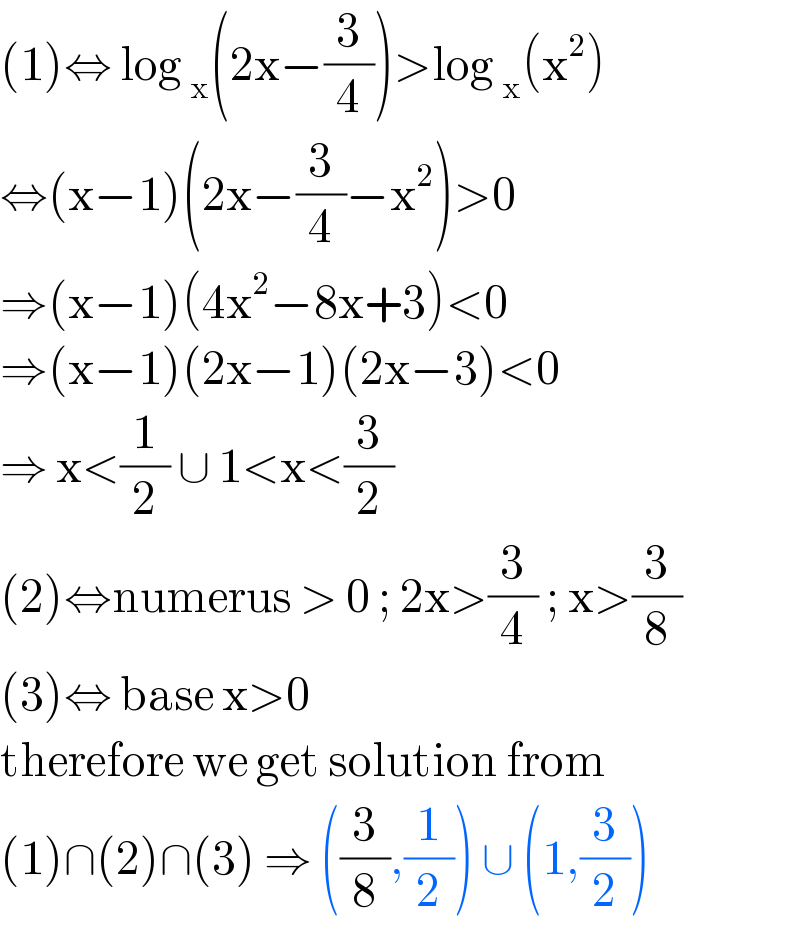
$$\left(\mathrm{1}\right)\Leftrightarrow\:\mathrm{log}\:_{\mathrm{x}} \left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{log}\:_{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{x}^{\mathrm{2}} \right)>\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{3}\right)<\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{2x}−\mathrm{3}\right)<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}<\frac{\mathrm{1}}{\mathrm{2}}\:\cup\:\mathrm{1}<\mathrm{x}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{numerus}\:>\:\mathrm{0}\:;\:\mathrm{2x}>\frac{\mathrm{3}}{\mathrm{4}}\:;\:\mathrm{x}>\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\:\mathrm{base}\:\mathrm{x}>\mathrm{0}\: \\ $$$$\mathrm{therefore}\:\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{from} \\ $$$$\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right)\cap\left(\mathrm{3}\right)\:\Rightarrow\:\left(\frac{\mathrm{3}}{\mathrm{8}},\frac{\mathrm{1}}{\mathrm{2}}\right)\:\cup\:\left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
Thanks for your efforts Sir
Answered by ebi last updated on 04/Nov/20
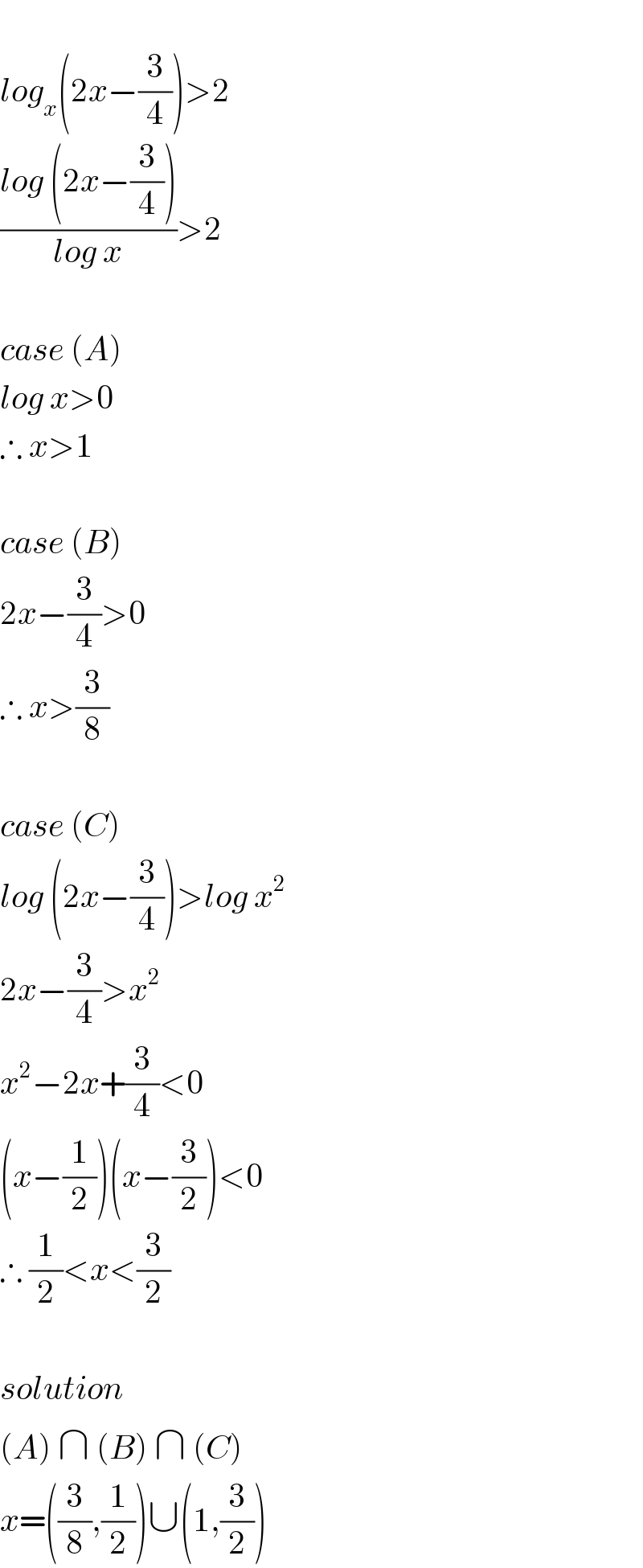
$$ \\ $$$${log}_{{x}} \left(\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{2} \\ $$$$\frac{{log}\:\left(\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{4}}\right)}{{log}\:{x}}>\mathrm{2} \\ $$$$ \\ $$$${case}\:\left({A}\right) \\ $$$${log}\:{x}>\mathrm{0} \\ $$$$\therefore\:{x}>\mathrm{1} \\ $$$$ \\ $$$${case}\:\left({B}\right) \\ $$$$\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{4}}>\mathrm{0} \\ $$$$\therefore\:{x}>\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$ \\ $$$${case}\:\left({C}\right) \\ $$$${log}\:\left(\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>{log}\:{x}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{4}}>{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{4}}<\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)<\mathrm{0} \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{2}}<{x}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$${solution} \\ $$$$\left({A}\right)\:\cap\:\left({B}\right)\:\cap\:\left({C}\right) \\ $$$${x}=\left(\frac{\mathrm{3}}{\mathrm{8}},\frac{\mathrm{1}}{\mathrm{2}}\right)\cup\left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
Thank you
Answered by Ar Brandon last updated on 04/Nov/20

$$\mathrm{log}_{\mathrm{x}} \left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{2}=\mathrm{log}_{\mathrm{x}} \mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{Domaine}:\:\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}>\mathrm{0}\:\wedge\:\mathrm{x}>\mathrm{0},\:\mathrm{x}\neq\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}>\frac{\mathrm{3}}{\mathrm{8}}\:\wedge\:\mathrm{x}>\mathrm{0},\:\mathrm{x}\neq\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{Domaine}\:\mathrm{is}\:\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\mathrm{1}\right)\cup\:\left(\mathrm{1},\:+\infty\right) \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{when}\:\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\mathrm{1}\right) \\ $$$$\mathrm{log}_{\mathrm{x}} \left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{log}_{\mathrm{x}} \mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}<\mathrm{x}^{\mathrm{2}} ,\:\mathrm{since}\:\mathrm{function}\:\mathrm{is}\:\mathrm{decreasing}\:\mathrm{for} \\ $$$$\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\mathrm{1}\right)\:\mathrm{ie}\:\mathrm{log}_{\mathrm{x}} \mathrm{a}>\mathrm{log}_{\mathrm{x}} \mathrm{b}\:\Rightarrow\:\mathrm{a}<\mathrm{b} \\ $$$$\Rightarrow\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{3}>\mathrm{0}\:\Rightarrow\:\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{2x}−\mathrm{3}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}\in\left(−\infty,\:\frac{\mathrm{1}}{\mathrm{2}}\right)\cup\left(\frac{\mathrm{3}}{\mathrm{2}},\:+\infty\right) \\ $$$$\mathrm{But}\:\mathrm{from}\:\mathrm{initial}\:\mathrm{condition}\:\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\mathrm{1}\right) \\ $$$$\mathrm{Therefore}\:\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{when}\:\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{x}} \left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{log}_{\mathrm{x}} \mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{4}}>\mathrm{x}^{\mathrm{2}} ,\:\mathrm{since}\:\mathrm{function}\:\mathrm{is}\:\mathrm{increasing}\:\mathrm{for} \\ $$$$\mathrm{x}>\mathrm{1}.\:\mathrm{ie}\:\mathrm{log}_{\mathrm{x}} \mathrm{a}>\mathrm{log}_{\mathrm{x}} \mathrm{b}\:\Rightarrow\:\mathrm{a}>\mathrm{b} \\ $$$$\Rightarrow\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{3}<\mathrm{0}\:\Rightarrow\:\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{2x}−\mathrm{3}\right)<\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{x}<\frac{\mathrm{3}}{\mathrm{2}}\: \\ $$$$\mathrm{But}\:\mathrm{from}\:\mathrm{initial}\:\mathrm{condition}\:\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{Therefore}\:\mathrm{x}\in\left(\mathrm{1},\:\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\mathrm{Combining}\:\mathrm{case}\:\mathrm{1}\:\mathrm{and}\:\mathrm{case}\:\mathrm{2}\:\mathrm{we}\:\mathrm{obtain} \\ $$$$\mathrm{x}\in\left(\frac{\mathrm{3}}{\mathrm{8}},\:\frac{\mathrm{1}}{\mathrm{2}}\right)\cup\left(\mathrm{1},\:\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
