
Question Number 120923 by bemath last updated on 04/Nov/20
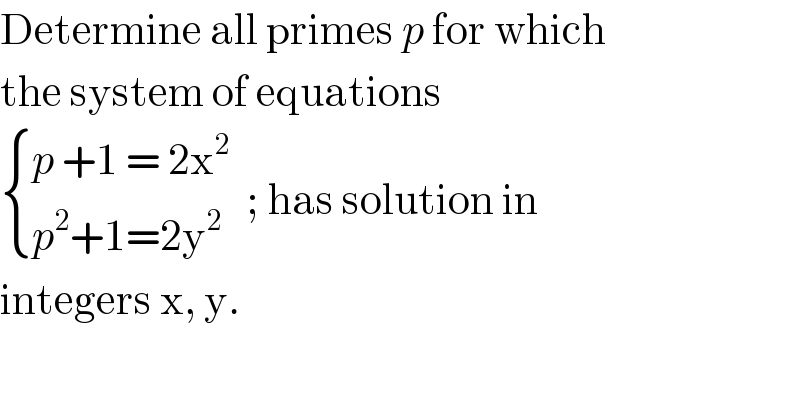
$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{primes}\:{p}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}\: \\ $$$$\begin{cases}{{p}\:+\mathrm{1}\:=\:\mathrm{2x}^{\mathrm{2}} }\\{{p}^{\mathrm{2}} +\mathrm{1}=\mathrm{2y}^{\mathrm{2}} \:\:}\end{cases}\:;\:\mathrm{has}\:\mathrm{solution}\:\mathrm{in} \\ $$$$\mathrm{integers}\:\mathrm{x},\:\mathrm{y}. \\ $$
Answered by liberty last updated on 04/Nov/20
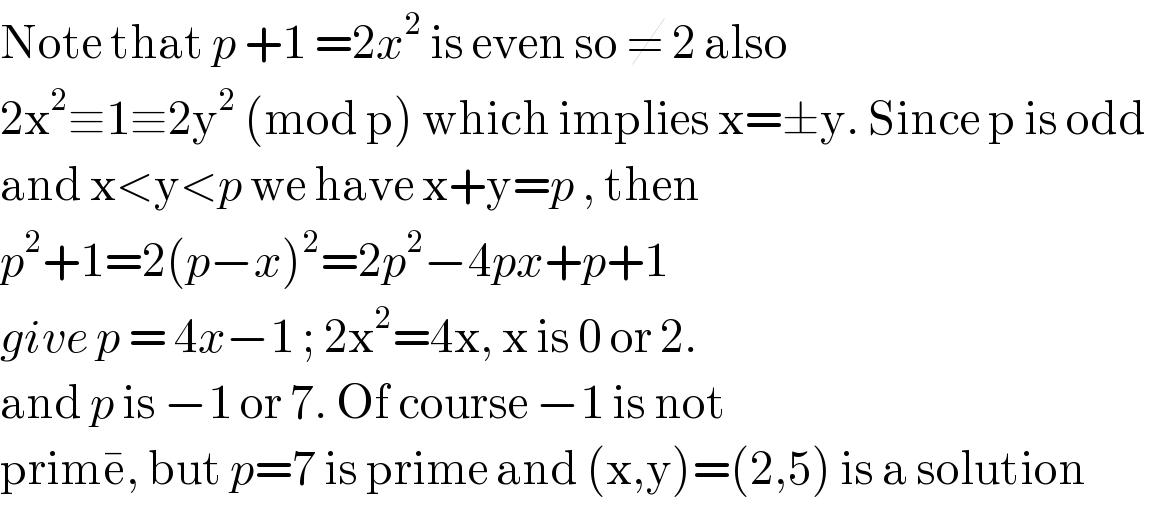
$$\mathrm{Note}\:\mathrm{that}\:{p}\:+\mathrm{1}\:=\mathrm{2}{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{even}\:\mathrm{so}\:\neq\:\mathrm{2}\:\mathrm{also} \\ $$$$\mathrm{2x}^{\mathrm{2}} \equiv\mathrm{1}\equiv\mathrm{2y}^{\mathrm{2}} \:\left(\mathrm{mod}\:\mathrm{p}\right)\:\mathrm{which}\:\mathrm{implies}\:\mathrm{x}=\pm\mathrm{y}.\:\mathrm{Since}\:\mathrm{p}\:\mathrm{is}\:\mathrm{odd}\: \\ $$$$\mathrm{and}\:\mathrm{x}<\mathrm{y}<{p}\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}+\mathrm{y}={p}\:,\:\mathrm{then}\: \\ $$$${p}^{\mathrm{2}} +\mathrm{1}=\mathrm{2}\left({p}−{x}\right)^{\mathrm{2}} =\mathrm{2}{p}^{\mathrm{2}} −\mathrm{4}{px}+{p}+\mathrm{1} \\ $$$${give}\:{p}\:=\:\mathrm{4}{x}−\mathrm{1}\:;\:\mathrm{2x}^{\mathrm{2}} =\mathrm{4x},\:\mathrm{x}\:\mathrm{is}\:\mathrm{0}\:\mathrm{or}\:\mathrm{2}. \\ $$$$\mathrm{and}\:{p}\:\mathrm{is}\:−\mathrm{1}\:\mathrm{or}\:\mathrm{7}.\:\mathrm{Of}\:\mathrm{course}\:−\mathrm{1}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{prim}\bar {\mathrm{e}},\:\mathrm{but}\:{p}=\mathrm{7}\:\mathrm{is}\:\mathrm{prime}\:\mathrm{and}\:\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{2},\mathrm{5}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$
