
Question Number 120895 by ajfour last updated on 03/Nov/20
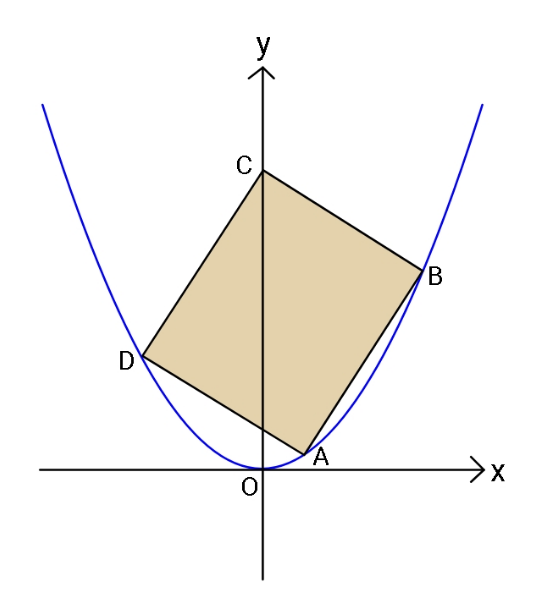
Commented by ajfour last updated on 05/Nov/20
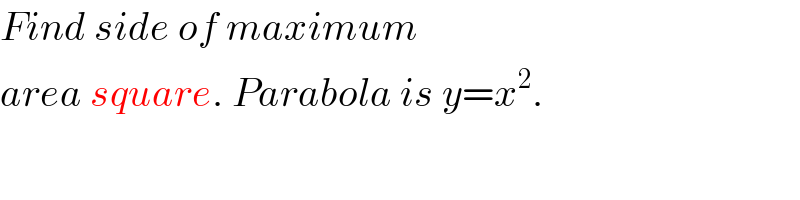
$${Find}\:{side}\:{of}\:{maximum} \\ $$$${area}\:{square}.\:{Parabola}\:{is}\:{y}={x}^{\mathrm{2}} . \\ $$
Commented by mr W last updated on 07/Nov/20

$${if}\:{square}\:{and}\:{C}\:{on}\:{y}−{axis},\:{i}\:{think} \\ $$$${there}\:{is}\:{only}\:{one}\:{solution}: \\ $$$${A}={O},\:{B}\left(\mathrm{1},\mathrm{1}\right),\:{C}\left(\mathrm{0},\mathrm{2}\right) \\ $$
Commented by ajfour last updated on 07/Nov/20
$${yes}\:{sir},\:{you}\:{must}\:{be}\:{correct}. \\ $$
Answered by MJS_new last updated on 03/Nov/20
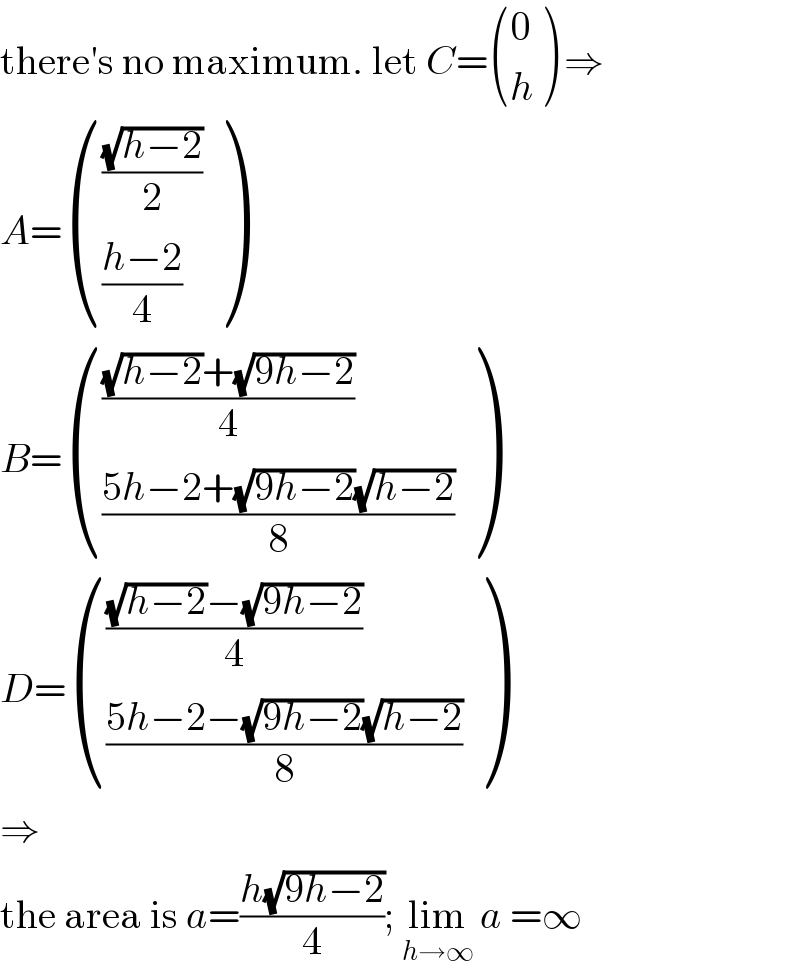
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{maximum}.\:\mathrm{let}\:{C}=\begin{pmatrix}{\mathrm{0}}\\{{h}}\end{pmatrix}\:\Rightarrow \\ $$$${A}=\begin{pmatrix}{\frac{\sqrt{{h}−\mathrm{2}}}{\mathrm{2}}}\\{\frac{{h}−\mathrm{2}}{\mathrm{4}}}\end{pmatrix}\: \\ $$$${B}=\begin{pmatrix}{\frac{\sqrt{{h}−\mathrm{2}}+\sqrt{\mathrm{9}{h}−\mathrm{2}}}{\mathrm{4}}}\\{\frac{\mathrm{5}{h}−\mathrm{2}+\sqrt{\mathrm{9}{h}−\mathrm{2}}\sqrt{{h}−\mathrm{2}}}{\mathrm{8}}}\end{pmatrix} \\ $$$${D}=\begin{pmatrix}{\frac{\sqrt{{h}−\mathrm{2}}−\sqrt{\mathrm{9}{h}−\mathrm{2}}}{\mathrm{4}}}\\{\frac{\mathrm{5}{h}−\mathrm{2}−\sqrt{\mathrm{9}{h}−\mathrm{2}}\sqrt{{h}−\mathrm{2}}}{\mathrm{8}}}\end{pmatrix} \\ $$$$\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{is}\:{a}=\frac{{h}\sqrt{\mathrm{9}{h}−\mathrm{2}}}{\mathrm{4}};\:\underset{{h}\rightarrow\infty} {\mathrm{lim}}\:{a}\:=\infty \\ $$
Commented by ajfour last updated on 03/Nov/20
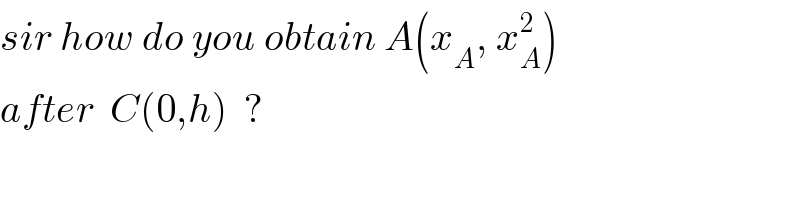
$${sir}\:{how}\:{do}\:{you}\:{obtain}\:{A}\left({x}_{{A}} ,\:{x}_{{A}} ^{\mathrm{2}} \right) \\ $$$${after}\:\:{C}\left(\mathrm{0},{h}\right)\:\:? \\ $$
Commented by MJS_new last updated on 03/Nov/20

$$\mathrm{I}\:\mathrm{started}\:\mathrm{with}\:{P}=\begin{pmatrix}{{x}_{{P}} }\\{{x}_{{P}} ^{\mathrm{2}} }\end{pmatrix}\:\mathrm{for}\:{A},\:{B},\:{D}\:\mathrm{and} \\ $$$${C}=\begin{pmatrix}{\mathrm{0}}\\{{h}}\end{pmatrix}\:.\:\mathrm{then}\:\mathrm{the}\:\mathrm{lines}\:\mathrm{must}\:\mathrm{be}\:\mathrm{parallel}\:/ \\ $$$$\mathrm{right}\:\mathrm{angled}\:\mathrm{in}\:\mathrm{pairs}.\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{from}\:\mathrm{there},\:{h}>\mathrm{0}\wedge{x}_{{B}} >{x}_{{A}} >\mathrm{0}\wedge{x}_{{D}} <\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to}\:\mathrm{take}\:\mathrm{2}\:\mathrm{different}\:\mathrm{solutions} \\ $$$$\mathrm{in}\:\mathrm{any}\:\mathrm{step}.\:\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}\:\mathrm{now}\:\mathrm{to} \\ $$$$\mathrm{write}\:\mathrm{it}\:\mathrm{out}\:\mathrm{in}\:\mathrm{detail} \\ $$
Commented by ajfour last updated on 03/Nov/20
$${thanks}\:{for}\:{as}\:{much},\:{Sir}. \\ $$
