
Question Number 120797 by Algoritm last updated on 02/Nov/20
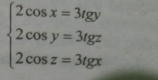
Commented by liberty last updated on 02/Nov/20

$$\begin{cases}{\mathrm{2cos}\:\mathrm{xcos}\:\mathrm{y}=\mathrm{3sin}\:\mathrm{y}}\\{\mathrm{2cos}\:\mathrm{ycos}\:\mathrm{z}=\mathrm{3sin}\:\mathrm{z}}\\{\mathrm{2cos}\:\mathrm{zcos}\:\mathrm{x}=\mathrm{3sin}\:\mathrm{x}}\end{cases}\rightarrow\mathrm{8cos}\:^{\mathrm{2}} \mathrm{xcos}\:^{\mathrm{2}} \mathrm{ycos}\:^{\mathrm{2}} \mathrm{z}=\mathrm{27sin}\:\mathrm{xsin}\:\mathrm{ysin}\:\mathrm{z} \\ $$$$\mathrm{by}\:\mathrm{symetric}\:\begin{cases}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}=\mathrm{3sin}\:\mathrm{x}}\\{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{y}=\mathrm{3sin}\:\mathrm{y}}\\{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{z}=\mathrm{3sin}\:\mathrm{z}}\end{cases} \\ $$$$\Rightarrow\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}=\mathrm{3sin}\:\mathrm{x}\:;\:\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2sin}\:\mathrm{x}−\mathrm{1}\right)\left(\mathrm{sin}\:\mathrm{x}+\mathrm{2}\right)=\mathrm{0}\Rightarrow\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{similarly}\:\mathrm{we}\:\mathrm{get}\:\rightarrow\begin{cases}{\mathrm{sin}\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{sin}\:\mathrm{z}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{checking}\:\begin{cases}{\mathrm{cos}\:\mathrm{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\mathrm{tan}\:\mathrm{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\end{cases}\:\Rightarrow\mathrm{2cos}\:\mathrm{x}=\mathrm{3tan}\:\mathrm{y} \\ $$$$\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\:\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\Rightarrow\sqrt{\mathrm{3}}\:=\:\sqrt{\mathrm{3}}\:\left(\mathrm{true}\right) \\ $$
