
Question Number 120679 by kaivan.ahmadi last updated on 02/Nov/20

$${h} \\ $$
Commented by bobhans last updated on 01/Nov/20
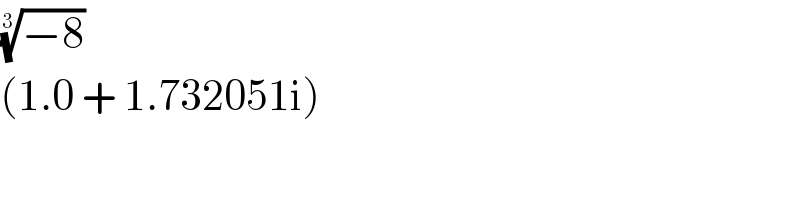
$$\sqrt[{\mathrm{3}}]{−\mathrm{8}}\: \\ $$$$\left(\mathrm{1}.\mathrm{0}\:+\:\mathrm{1}.\mathrm{732051i}\right) \\ $$
Commented by bobhans last updated on 01/Nov/20
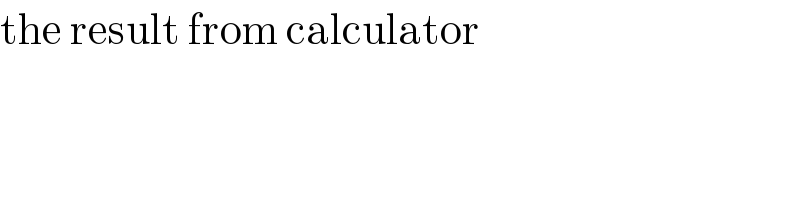
$$\mathrm{the}\:\mathrm{result}\:\mathrm{from}\:\mathrm{calculator} \\ $$
Commented by mathmax by abdo last updated on 02/Nov/20
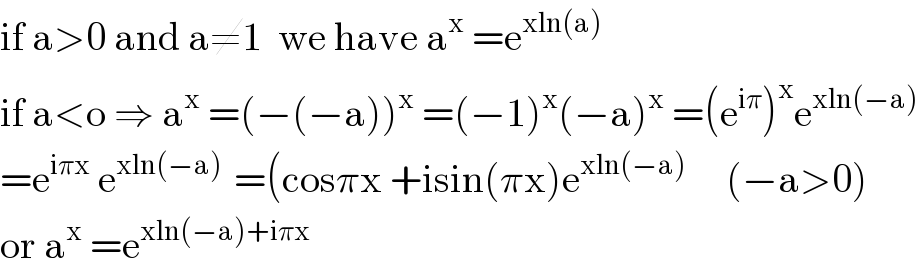
$$\mathrm{if}\:\mathrm{a}>\mathrm{0}\:\mathrm{and}\:\mathrm{a}\neq\mathrm{1}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}^{\mathrm{x}} \:=\mathrm{e}^{\mathrm{xln}\left(\mathrm{a}\right)} \\ $$$$\mathrm{if}\:\mathrm{a}<\mathrm{o}\:\Rightarrow\:\mathrm{a}^{\mathrm{x}} \:=\left(−\left(−\mathrm{a}\right)\right)^{\mathrm{x}} \:=\left(−\mathrm{1}\right)^{\mathrm{x}} \left(−\mathrm{a}\right)^{\mathrm{x}} \:=\left(\mathrm{e}^{\mathrm{i}\pi} \right)^{\mathrm{x}} \mathrm{e}^{\mathrm{xln}\left(−\mathrm{a}\right)} \\ $$$$=\mathrm{e}^{\mathrm{i}\pi\mathrm{x}} \:\mathrm{e}^{\mathrm{xln}\left(−\mathrm{a}\right)\:} \:=\left(\mathrm{cos}\pi\mathrm{x}\:+\mathrm{isin}\left(\pi\mathrm{x}\right)\mathrm{e}^{\mathrm{xln}\left(−\mathrm{a}\right)} \:\:\:\:\:\left(−\mathrm{a}>\mathrm{0}\right)\right. \\ $$$$\mathrm{or}\:\mathrm{a}^{\mathrm{x}} \:=\mathrm{e}^{\mathrm{xln}\left(−\mathrm{a}\right)+\mathrm{i}\pi\mathrm{x}} \\ $$
Answered by MJS_new last updated on 01/Nov/20

$$\mathrm{but}\:\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\boldsymbol{{is}}\:\mathrm{defined}. \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{2}\:\mathrm{definitions} \\ $$$$\left(\mathrm{1}\right)\:{z}\in\mathbb{C},\:{r}\in\mathbb{R}^{+} :\:{z}^{\frac{\mathrm{1}}{{n}}} =\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)^{\frac{\mathrm{1}}{{n}}} ={r}^{\frac{\mathrm{1}}{{n}}} \mathrm{e}^{\mathrm{i}\frac{\theta}{{n}}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{for}\:\theta=\pi\wedge\:{n}=\mathrm{2}{k}+\mathrm{1}\:\mathrm{we}\:\mathrm{have}\:{z}={r}\mathrm{e}^{\mathrm{i}\pi} =−{r} \\ $$$$\:\:\:\:\:\mathrm{and}\:\mathrm{define}\:{z}^{\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}} =\left(−{r}\right)^{\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}} =−\left({r}^{\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}} \right) \\ $$$$\mathrm{this}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{definition}\:\mathrm{is}\:``\mathrm{older}''\:\mathrm{because}\:\mathrm{in} \\ $$$$\mathrm{basic}\:\mathrm{mathematics}\:\mathrm{it}'\mathrm{s}\:\mathrm{common}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it} \\ $$$$\Rightarrow\:\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\begin{cases}{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}}\\{−\mathrm{2}}\end{cases} \\ $$
Commented by bobhans last updated on 01/Nov/20
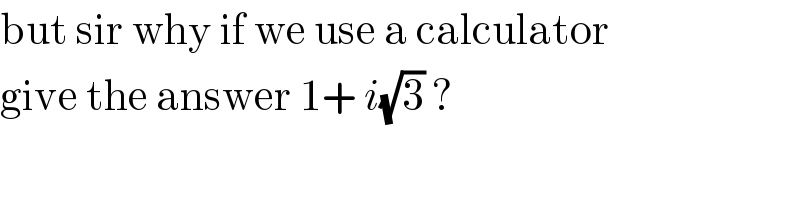
$$\mathrm{but}\:\mathrm{sir}\:\mathrm{why}\:\mathrm{if}\:\mathrm{we}\:\mathrm{use}\:\mathrm{a}\:\mathrm{calculator} \\ $$$$\mathrm{give}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{1}+\:{i}\sqrt{\mathrm{3}}\:? \\ $$
Commented by MJS_new last updated on 02/Nov/20

$$\mathrm{depends}\:\mathrm{on}\:\mathrm{the}\:\mathrm{calculator}.\:\mathrm{the}\:\mathrm{ones}\:\mathrm{for} \\ $$$$\mathrm{high}\:\mathrm{schools}\:\mathrm{should}\:\mathrm{give}\:−\mathrm{2},\:\mathrm{the}\:\mathrm{ones}\:\mathrm{for} \\ $$$$\mathrm{university}\:\mathrm{give}\:\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i} \\ $$$$\mathrm{I}\:\mathrm{guess}\:\mathrm{using}\:\mathrm{the}\:\mathrm{exceptions}\:\sqrt[{\mathrm{3}}]{−\mathrm{27}}=−\mathrm{3}; \\ $$$$\sqrt[{\mathrm{5}}]{−\mathrm{32}}=−\mathrm{2}\:{etc}.\:\mathrm{makes}\:\mathrm{it}\:\mathrm{impossible}\:\mathrm{to} \\ $$$$\mathrm{get}\:\mathrm{a}\:\mathrm{result}\:\mathrm{for}\:\mathrm{calculations}\:\mathrm{like}\:\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{exeptions}\:\mathrm{do}\:\mathrm{harm}\:\mathrm{to}\:\mathrm{functions} \\ $$$$\mathrm{like}\:{f}\left({x}\right):\:{y}=\left(−\mathrm{1}\right)^{{x}} \:\mathrm{for}\:{x}\in\mathbb{R}\wedge{y}\in\mathbb{C} \\ $$$$\Rightarrow\:\mathrm{most}\:\mathrm{advanced}\:\mathrm{calculators}\:\mathrm{use} \\ $$$${z}^{{p}+{q}\mathrm{i}} =\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)^{{p}+{q}\mathrm{i}} ={r}^{{p}+{q}\mathrm{i}} \mathrm{e}^{−{q}\theta+\mathrm{ip}\theta} = \\ $$$$=\frac{{r}^{{p}} }{\mathrm{e}^{{q}\theta} }\mathrm{e}^{{i}\left({p}\theta+{q}\mathrm{ln}\:{r}\right)} \:\mathrm{which}\:\mathrm{for}\:{q}=\mathrm{0}\:\mathrm{gives}\:{r}^{{p}} \mathrm{e}^{\mathrm{i}{p}\theta} \\ $$
Commented by bobhans last updated on 02/Nov/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by malwaan last updated on 02/Nov/20
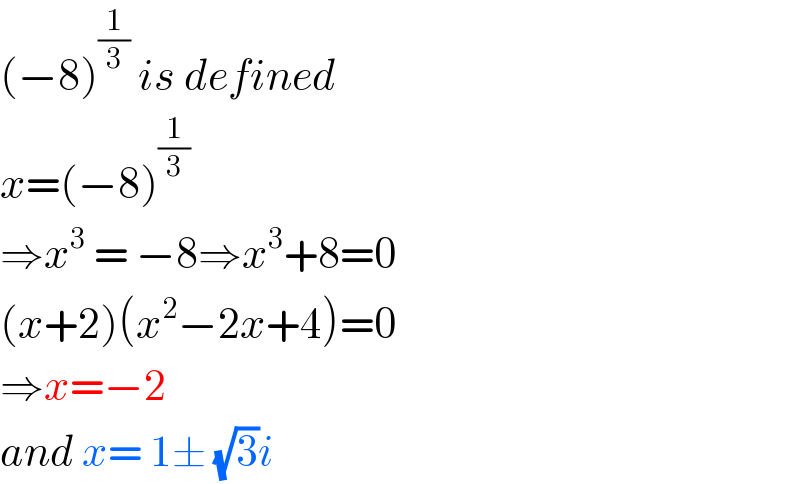
$$\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{is}\:{defined} \\ $$$${x}=\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\Rightarrow{x}^{\mathrm{3}} \:=\:−\mathrm{8}\Rightarrow{x}^{\mathrm{3}} +\mathrm{8}=\mathrm{0} \\ $$$$\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{2} \\ $$$${and}\:{x}=\:\mathrm{1}\pm\:\sqrt{\mathrm{3}}{i} \\ $$
