
Question Number 120601 by Don08q last updated on 01/Nov/20

$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:{x}\:\mathrm{for}\: \\ $$$$\:\mathrm{which}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\mathrm{the}\:\mathrm{binomial} \\ $$$$\:\left(\mathrm{2}\:−\:\mathrm{3}{x}\right)^{−\mathrm{4}} \:\mathrm{is}\:\mathrm{valid}.\: \\ $$$$\:{I}\:{need}\:{help}\:{with}\:{explanation}\:{please} \\ $$
Answered by Ar Brandon last updated on 01/Nov/20
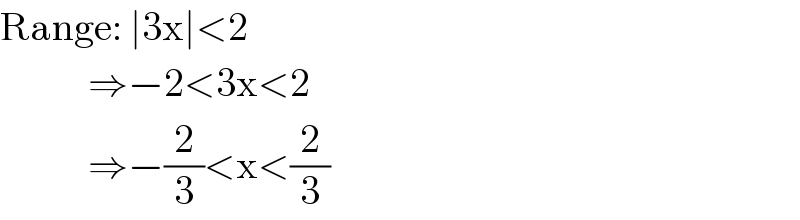
$$\mathrm{Range}:\:\mid\mathrm{3x}\mid<\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{2}<\mathrm{3x}<\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\frac{\mathrm{2}}{\mathrm{3}}<\mathrm{x}<\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Don08q last updated on 01/Nov/20
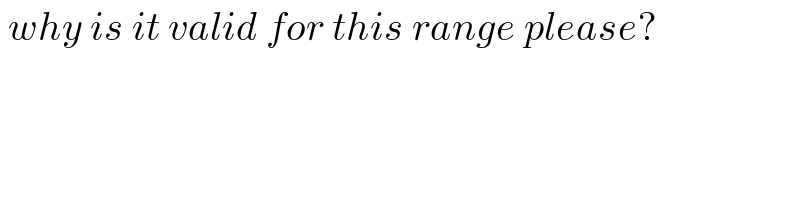
$$\:{why}\:{is}\:{it}\:{valid}\:{for}\:{this}\:{range}\:{please}? \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 01/Nov/20
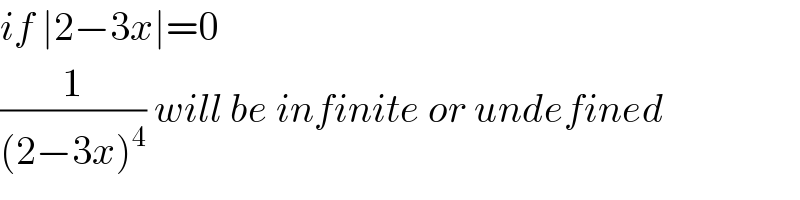
$${if}\:\mid\mathrm{2}−\mathrm{3}{x}\mid=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{3}{x}\right)^{\mathrm{4}} }\:{will}\:{be}\:{infinite}\:{or}\:{undefined} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Nov/20
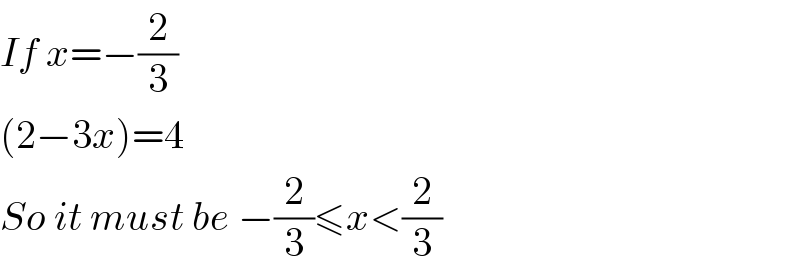
$${If}\:{x}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left(\mathrm{2}−\mathrm{3}{x}\right)=\mathrm{4} \\ $$$${So}\:{it}\:{must}\:{be}\:−\frac{\mathrm{2}}{\mathrm{3}}\leqslant{x}<\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Don08q last updated on 02/Nov/20
$${Alright}.\:{Thank}\:{you}. \\ $$
