
Question Number 120395 by bramlexs22 last updated on 31/Oct/20
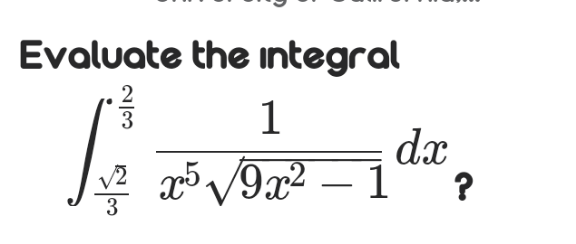
Answered by Olaf last updated on 31/Oct/20
![u = 9x^2 , du = 18xdx = 6u^(1/2) dx I = ∫_2 ^4 (1/(((u/3))^(5/2) (√(u−1)))).(du/(6u^(1/2) )) I = ((3(√3))/2)∫_2 ^4 (du/(u^3 .(√(u−1)))) By parts : I = ((3(√3))/2)[((√(x−1))/(2x^2 ))+((3(√(x−1)))/(4x))+(3/4)arctan((√(x−1)))]_2 ^4 I = ((3(√3))/2)[((√3)/(32))+((3(√3))/(16))+(3/4)arctan((√3))−(1/8)−(3/8)−(3/4)arctan(1)] I = ((3(√3))/2)[((7(√3))/(32))−(1/2)+(π/4)−((3π)/(16))] I = ((3(√3))/2)[((7(√3))/(32))−(1/2)+(π/4)] I = ((63)/(64))−((3(√3))/4)+((3(√3)π)/8)](Q120407.png)
$$ \\ $$$${u}\:=\:\mathrm{9}{x}^{\mathrm{2}} ,\:{du}\:=\:\mathrm{18}{xdx}\:=\:\mathrm{6}{u}^{\mathrm{1}/\mathrm{2}} {dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\mathrm{1}}{\left(\frac{{u}}{\mathrm{3}}\right)^{\mathrm{5}/\mathrm{2}} \sqrt{{u}−\mathrm{1}}}.\frac{{du}}{\mathrm{6}{u}^{\mathrm{1}/\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{{du}}{{u}^{\mathrm{3}} .\sqrt{{u}−\mathrm{1}}} \\ $$$$\mathrm{By}\:\mathrm{parts}\:: \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\left[\frac{\sqrt{{x}−\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{{x}−\mathrm{1}}}{\mathrm{4}{x}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{arctan}\left(\sqrt{{x}−\mathrm{1}}\right)\right]_{\mathrm{2}} ^{\mathrm{4}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{32}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{arctan}\left(\sqrt{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{arctan}\left(\mathrm{1}\right)\right] \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\left[\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}−\frac{\mathrm{3}\pi}{\mathrm{16}}\right] \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\left[\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right] \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{63}}{\mathrm{64}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}\pi}{\mathrm{8}} \\ $$
Answered by Lordose last updated on 31/Oct/20
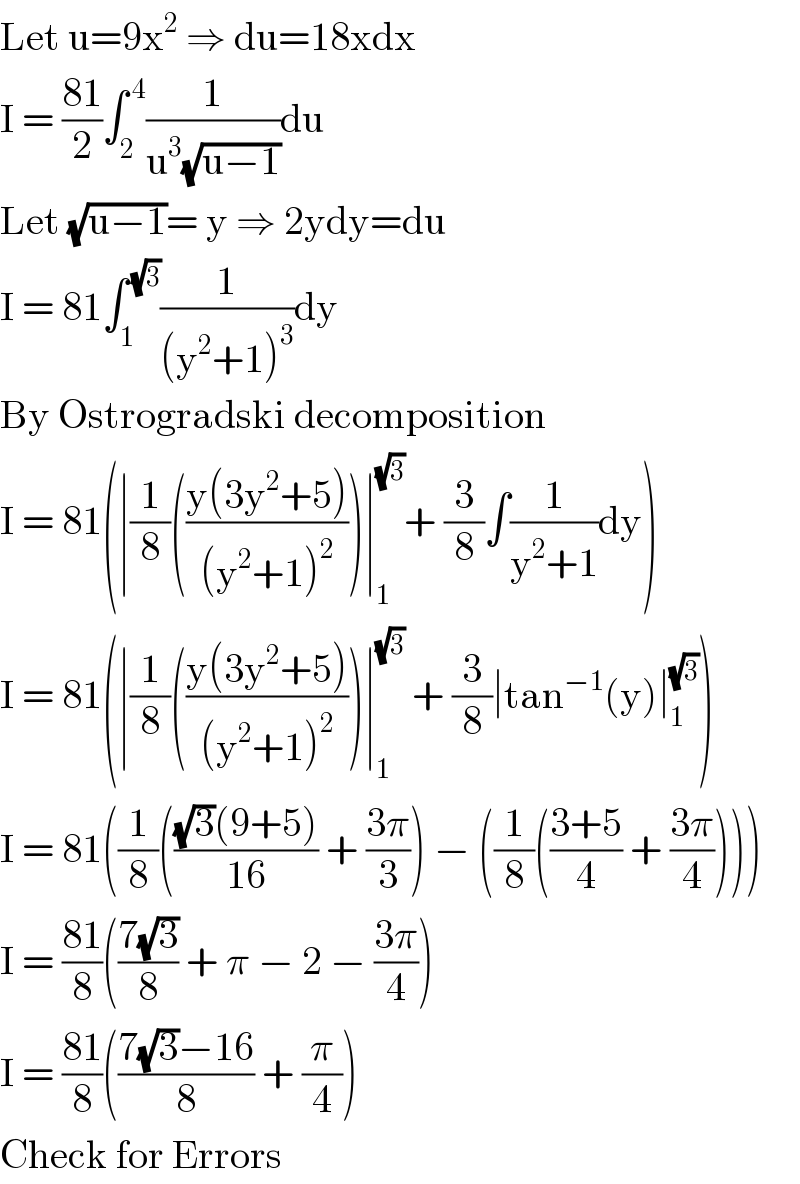
$$\mathrm{Let}\:\mathrm{u}=\mathrm{9x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{du}=\mathrm{18xdx} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{81}}{\mathrm{2}}\int_{\mathrm{2}} ^{\:\mathrm{4}} \frac{\mathrm{1}}{\mathrm{u}^{\mathrm{3}} \sqrt{\mathrm{u}−\mathrm{1}}}\mathrm{du} \\ $$$$\mathrm{Let}\:\sqrt{\mathrm{u}−\mathrm{1}}=\:\mathrm{y}\:\Rightarrow\:\mathrm{2ydy}=\mathrm{du} \\ $$$$\mathrm{I}\:=\:\mathrm{81}\int_{\mathrm{1}} ^{\:\sqrt{\mathrm{3}}} \frac{\mathrm{1}}{\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dy} \\ $$$$\mathrm{By}\:\mathrm{Ostrogradski}\:\mathrm{decomposition} \\ $$$$\mathrm{I}\:=\:\mathrm{81}\left(\mid\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{y}\left(\mathrm{3y}^{\mathrm{2}} +\mathrm{5}\right)}{\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\mid_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} +\:\frac{\mathrm{3}}{\mathrm{8}}\int\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\mathrm{dy}\right) \\ $$$$\mathrm{I}\:=\:\mathrm{81}\left(\mid\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{y}\left(\mathrm{3y}^{\mathrm{2}} +\mathrm{5}\right)}{\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\mid_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:+\:\frac{\mathrm{3}}{\mathrm{8}}\mid\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)\mid_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \right) \\ $$$$\mathrm{I}\:=\:\mathrm{81}\left(\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\sqrt{\mathrm{3}}\left(\mathrm{9}+\mathrm{5}\right)}{\mathrm{16}}\:+\:\frac{\mathrm{3}\pi}{\mathrm{3}}\right)\:−\:\left(\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{3}+\mathrm{5}}{\mathrm{4}}\:+\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\right)\right) \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{81}}{\mathrm{8}}\left(\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}\:+\:\pi\:−\:\mathrm{2}\:−\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{81}}{\mathrm{8}}\left(\frac{\mathrm{7}\sqrt{\mathrm{3}}−\mathrm{16}}{\mathrm{8}}\:+\:\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{Check}\:\mathrm{for}\:\mathrm{Errors} \\ $$
Answered by bobhans last updated on 31/Oct/20
![I = ∫ (dx/(x^5 (√(9x^2 −1)))) ; [ sec θ=3x ] I= ∫ ((sec θ.tan θ)/(3((1/3)sec θ)^5 .tan θ)) dθ I= ∫ 81cos^4 θ dθ = ∫81(1+2cos 2θ+cos^2 2θ)dθ I= ((81)/8)(3θ+2sin 2θ+(1/4)sin 4θ)+ c thus ∫_(π/4) ^(π/3) (dx/(x^5 (√(9x^2 +1)))) = ((81)/8)(2π−16+7(√3))](Q120424.png)
$${I}\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{5}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}}\:\:;\:\left[\:\mathrm{sec}\:\theta=\mathrm{3}{x}\:\right] \\ $$$${I}=\:\int\:\frac{\mathrm{sec}\:\theta.\mathrm{tan}\:\theta}{\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\:\theta\right)^{\mathrm{5}} .\mathrm{tan}\:\theta}\:{d}\theta \\ $$$${I}=\:\int\:\mathrm{81cos}\:^{\mathrm{4}} \theta\:{d}\theta\:=\:\int\mathrm{81}\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{2}\theta+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta\right){d}\theta \\ $$$${I}=\:\frac{\mathrm{81}}{\mathrm{8}}\left(\mathrm{3}\theta+\mathrm{2sin}\:\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{4}\theta\right)+\:{c} \\ $$$${thus}\:\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\:\frac{{dx}}{{x}^{\mathrm{5}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}}}\:=\:\frac{\mathrm{81}}{\mathrm{8}}\left(\mathrm{2}\pi−\mathrm{16}+\mathrm{7}\sqrt{\mathrm{3}}\right) \\ $$
