
Question Number 120185 by mr W last updated on 29/Oct/20
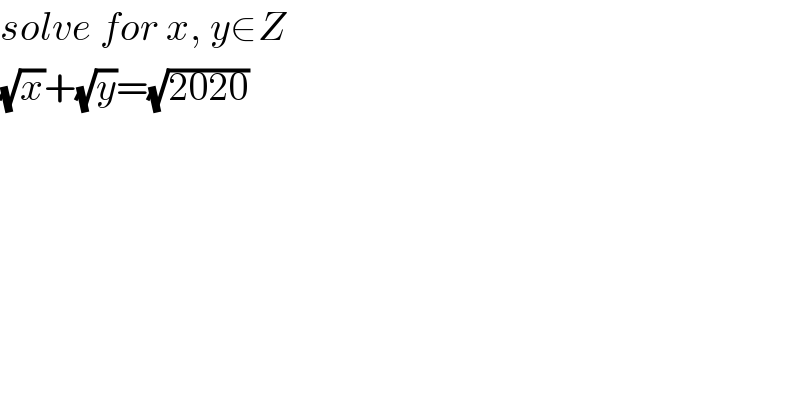
$${solve}\:{for}\:{x},\:{y}\in{Z} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{\mathrm{2020}} \\ $$
Answered by floor(10²Eta[1]) last updated on 29/Oct/20

$$\sqrt{\mathrm{y}}=\sqrt{\mathrm{2020}}−\sqrt{\mathrm{x}} \\ $$$$\left(\mathrm{y}=\mathrm{2020}+\mathrm{x}−\mathrm{2}\sqrt{\mathrm{2020x}}\right)\:\in\mathbb{Z} \\ $$$$\Rightarrow\sqrt{\mathrm{2020x}}\:\in\mathbb{Z} \\ $$$$\sqrt{\mathrm{2020x}}=\mathrm{2}\sqrt{\mathrm{505x}} \\ $$$$\Rightarrow\sqrt{\mathrm{505x}}\:\in\mathbb{Z}\Rightarrow\mathrm{x}=\mathrm{505a}^{\mathrm{2}} ,\:\mathrm{a}\in\mathbb{Z} \\ $$$$\mathrm{Similarly}:\:\mathrm{y}=\mathrm{505b}^{\mathrm{2}} ,\:\mathrm{b}\in\mathbb{Z} \\ $$$$\sqrt{\mathrm{505a}^{\mathrm{2}} }+\sqrt{\mathrm{505b}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{505}} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{0},\:\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{1},\:\mathrm{b}=\mathrm{1} \\ $$$$\mathrm{a}=\mathrm{2},\:\mathrm{b}=\mathrm{0} \\ $$$$\left(\mathrm{x},\:\mathrm{y}\right)\in\left\{\left(\mathrm{0},\:\mathrm{2020}\right),\:\left(\mathrm{505},\:\mathrm{505}\right),\:\left(\mathrm{2020},\:\mathrm{0}\right)\right\} \\ $$
Commented by mr W last updated on 30/Oct/20

$${thanks}! \\ $$
