
Question Number 120131 by huotpat last updated on 29/Oct/20
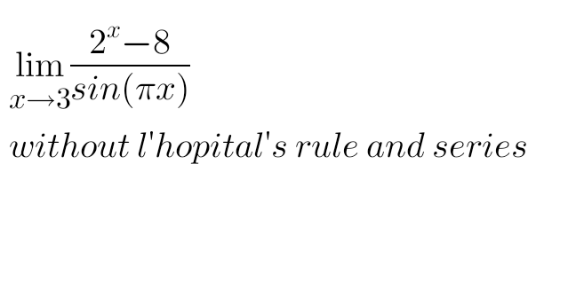
Commented by Dwaipayan Shikari last updated on 29/Oct/20
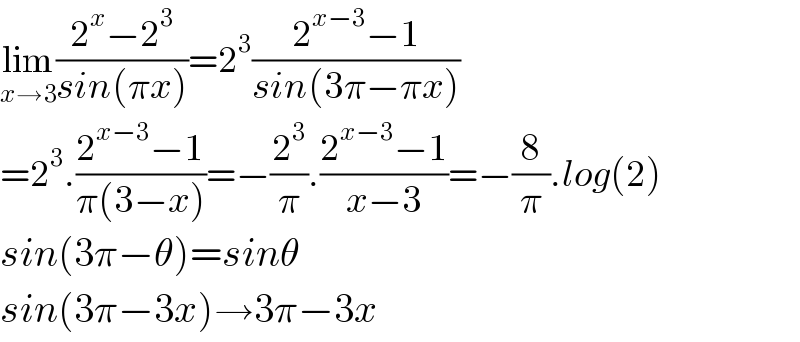
$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\mathrm{2}^{{x}} −\mathrm{2}^{\mathrm{3}} }{{sin}\left(\pi{x}\right)}=\mathrm{2}^{\mathrm{3}} \frac{\mathrm{2}^{{x}−\mathrm{3}} −\mathrm{1}}{{sin}\left(\mathrm{3}\pi−\pi{x}\right)} \\ $$$$=\mathrm{2}^{\mathrm{3}} .\frac{\mathrm{2}^{{x}−\mathrm{3}} −\mathrm{1}}{\pi\left(\mathrm{3}−{x}\right)}=−\frac{\mathrm{2}^{\mathrm{3}} }{\pi}.\frac{\mathrm{2}^{{x}−\mathrm{3}} −\mathrm{1}}{{x}−\mathrm{3}}=−\frac{\mathrm{8}}{\pi}.{log}\left(\mathrm{2}\right) \\ $$$${sin}\left(\mathrm{3}\pi−\theta\right)={sin}\theta \\ $$$${sin}\left(\mathrm{3}\pi−\mathrm{3}{x}\right)\rightarrow\mathrm{3}\pi−\mathrm{3}{x} \\ $$
Answered by Bird last updated on 29/Oct/20
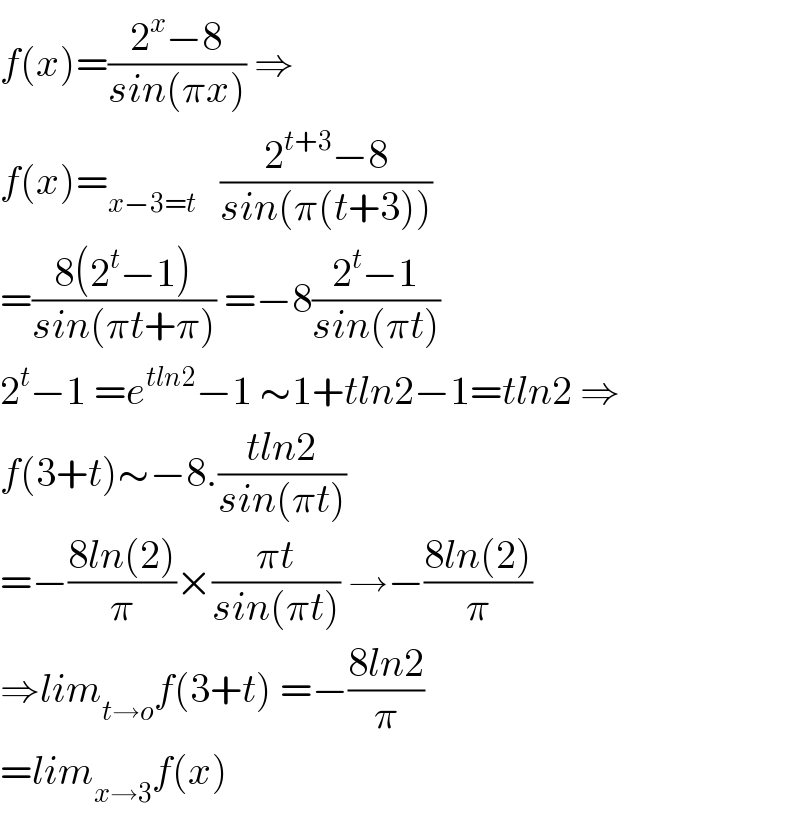
$${f}\left({x}\right)=\frac{\mathrm{2}^{{x}} −\mathrm{8}}{{sin}\left(\pi{x}\right)}\:\Rightarrow \\ $$$${f}\left({x}\right)=_{{x}−\mathrm{3}={t}} \:\:\:\frac{\mathrm{2}^{{t}+\mathrm{3}} −\mathrm{8}}{{sin}\left(\pi\left({t}+\mathrm{3}\right)\right)} \\ $$$$=\frac{\mathrm{8}\left(\mathrm{2}^{{t}} −\mathrm{1}\right)}{{sin}\left(\pi{t}+\pi\right)}\:=−\mathrm{8}\frac{\mathrm{2}^{{t}} −\mathrm{1}}{{sin}\left(\pi{t}\right)} \\ $$$$\mathrm{2}^{{t}} −\mathrm{1}\:={e}^{{tln}\mathrm{2}} −\mathrm{1}\:\sim\mathrm{1}+{tln}\mathrm{2}−\mathrm{1}={tln}\mathrm{2}\:\Rightarrow \\ $$$${f}\left(\mathrm{3}+{t}\right)\sim−\mathrm{8}.\frac{{tln}\mathrm{2}}{{sin}\left(\pi{t}\right)} \\ $$$$=−\frac{\mathrm{8}{ln}\left(\mathrm{2}\right)}{\pi}×\frac{\pi{t}}{{sin}\left(\pi{t}\right)}\:\rightarrow−\frac{\mathrm{8}{ln}\left(\mathrm{2}\right)}{\pi} \\ $$$$\Rightarrow{lim}_{{t}\rightarrow{o}} {f}\left(\mathrm{3}+{t}\right)\:=−\frac{\mathrm{8}{ln}\mathrm{2}}{\pi} \\ $$$$={lim}_{{x}\rightarrow\mathrm{3}} {f}\left({x}\right) \\ $$
