
Question Number 12008 by tawa last updated on 09/Apr/17

Commented by chux last updated on 09/Apr/17

$$\mathrm{which}\:\mathrm{country}\:\mathrm{do}\:\mathrm{you}\:\mathrm{come}\:\mathrm{from}\:\mathrm{tawa} \\ $$
Answered by ajfour last updated on 09/Apr/17
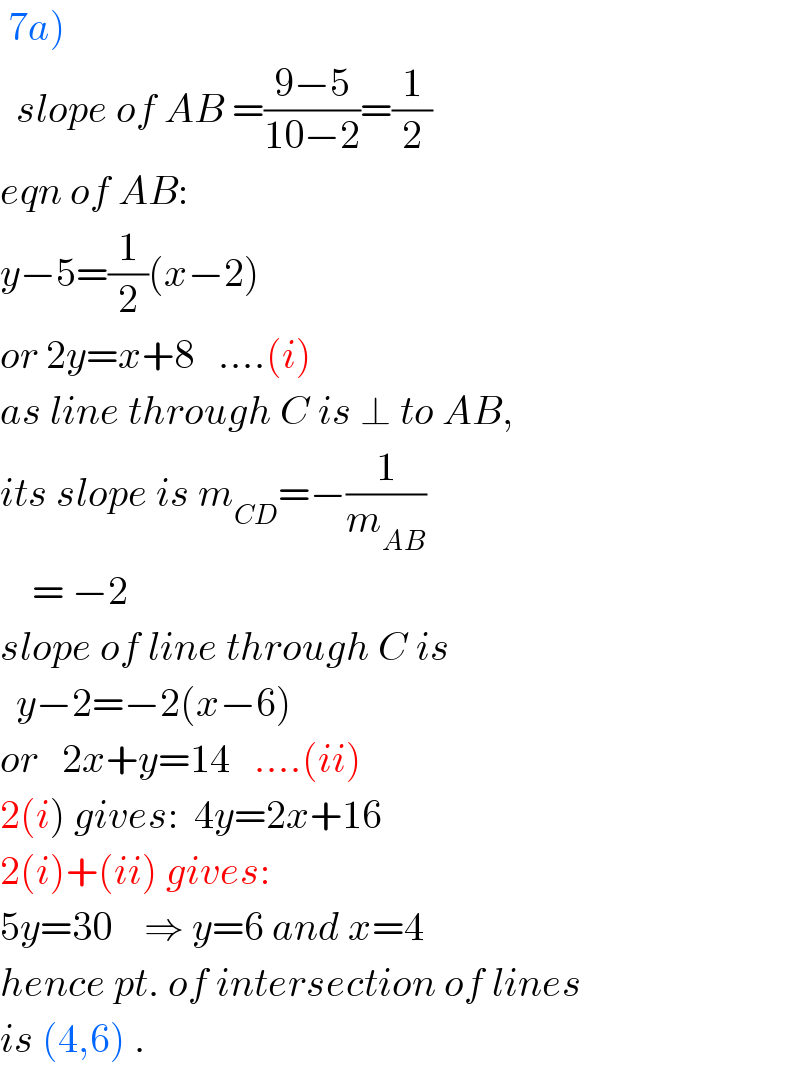
$$\left.\:\mathrm{7}{a}\right) \\ $$$$\:\:{slope}\:{of}\:{AB}\:=\frac{\mathrm{9}−\mathrm{5}}{\mathrm{10}−\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${eqn}\:{of}\:{AB}: \\ $$$${y}−\mathrm{5}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{2}\right) \\ $$$${or}\:\mathrm{2}{y}={x}+\mathrm{8}\:\:\:....\left({i}\right) \\ $$$${as}\:{line}\:{through}\:{C}\:{is}\:\bot\:{to}\:{AB}, \\ $$$${its}\:{slope}\:{is}\:{m}_{{CD}} =−\frac{\mathrm{1}}{{m}_{{AB}} } \\ $$$$\:\:\:\:=\:−\mathrm{2} \\ $$$${slope}\:{of}\:{line}\:{through}\:{C}\:{is} \\ $$$$\:\:{y}−\mathrm{2}=−\mathrm{2}\left({x}−\mathrm{6}\right) \\ $$$${or}\:\:\:\mathrm{2}{x}+{y}=\mathrm{14}\:\:\:....\left({ii}\right) \\ $$$$\mathrm{2}\left({i}\right)\:{gives}:\:\:\mathrm{4}{y}=\mathrm{2}{x}+\mathrm{16} \\ $$$$\mathrm{2}\left({i}\right)+\left({ii}\right)\:{gives}: \\ $$$$\mathrm{5}{y}=\mathrm{30}\:\:\:\:\Rightarrow\:{y}=\mathrm{6}\:{and}\:{x}=\mathrm{4} \\ $$$${hence}\:{pt}.\:{of}\:{intersection}\:{of}\:{lines} \\ $$$${is}\:\left(\mathrm{4},\mathrm{6}\right)\:. \\ $$
Commented by tawa last updated on 09/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by ajfour last updated on 09/Apr/17
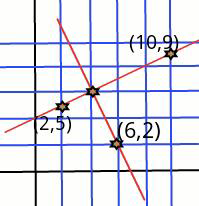
Commented by tawa last updated on 09/Apr/17
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\: \\ $$
