
Previous in Differential Equation Next in Differential Equation
Question Number 120058 by bramlexs22 last updated on 29/Oct/20
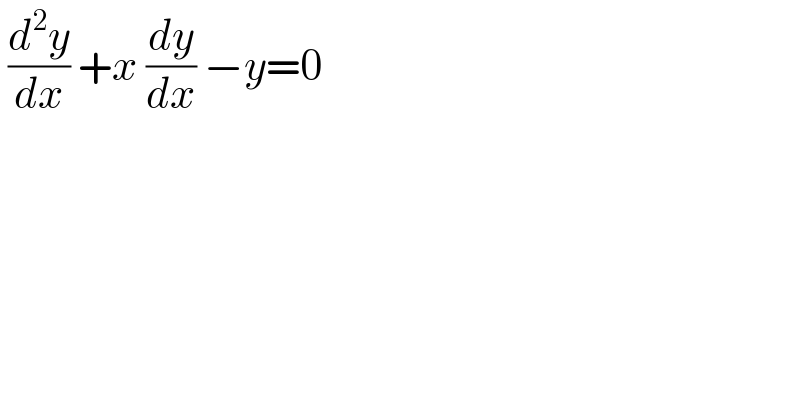
$$\:\frac{{d}^{\mathrm{2}} {y}}{{dx}}\:+{x}\:\frac{{dy}}{{dx}}\:−{y}=\mathrm{0} \\ $$
Answered by Olaf last updated on 29/Oct/20
![y′′+xy′−y = 0 (1) y = xu y′ = xu′+u y′′ = xu′′+2u′ (1) : xu′′+2u′+x(xu′+u)−xu = 0 xu′′+2u′+x^2 u′ = 0 ((u′′)/(u′)) = −((2+x^2 )/x) = −(2/x)−x ln∣u′∣ = −2ln∣x∣−(x^2 /2)+C_1 u′ = C_2 e^(ln(1/x^2 )) e^(−(x^2 /2)) = (C_2 /x^2 )e^(−(x^2 /2)) u = −C_2 [(e^(−(x^2 /2)) /x)+(√(π/2))erf((x/( (√2))))]+C_3 (By parts) y = ux = −C_2 [e^(−(x^2 /2)) +(√(π/2))xerf((x/( (√2))))]+C_3 x](Q120079.png)
$$ \\ $$$${y}''+{xy}'−{y}\:=\:\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$${y}\:=\:{xu} \\ $$$${y}'\:=\:{xu}'+{u} \\ $$$${y}''\:=\:{xu}''+\mathrm{2}{u}' \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\::\:{xu}''+\mathrm{2}{u}'+{x}\left({xu}'+{u}\right)−{xu}\:=\:\mathrm{0} \\ $$$${xu}''+\mathrm{2}{u}'+{x}^{\mathrm{2}} {u}'\:=\:\mathrm{0} \\ $$$$\frac{{u}''}{{u}'}\:=\:−\frac{\mathrm{2}+{x}^{\mathrm{2}} }{{x}}\:=\:−\frac{\mathrm{2}}{{x}}−{x} \\ $$$$\mathrm{ln}\mid{u}'\mid\:=\:−\mathrm{2ln}\mid{x}\mid−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{C}_{\mathrm{1}} \\ $$$${u}'\:=\:\mathrm{C}_{\mathrm{2}} {e}^{\mathrm{ln}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} {e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:=\:\frac{\mathrm{C}_{\mathrm{2}} }{{x}^{\mathrm{2}} }{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${u}\:=\:−\mathrm{C}_{\mathrm{2}} \left[\frac{{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{{x}}+\sqrt{\frac{\pi}{\mathrm{2}}}\mathrm{erf}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right]+\mathrm{C}_{\mathrm{3}} \\ $$$$\left(\mathrm{By}\:\mathrm{parts}\right) \\ $$$$ \\ $$$${y}\:=\:{ux}\:=\:−\mathrm{C}_{\mathrm{2}} \left[{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +\sqrt{\frac{\pi}{\mathrm{2}}}{x}\mathrm{erf}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right]+\mathrm{C}_{\mathrm{3}} {x} \\ $$
