
Question Number 119996 by behi83417@gmail.com last updated on 28/Oct/20
![{ ((x^3 +y^2 =a)),((x^2 +y^3 =b)) :} [solve for:x,y,a≠b∈R]](Q119996.png)
$$\begin{cases}{\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{y}}^{\mathrm{2}} =\boldsymbol{{a}}}\\{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{3}} =\boldsymbol{{b}}}\end{cases}\:\:\:\left[\boldsymbol{{solve}}\:\boldsymbol{{for}}:\mathrm{x},\mathrm{y},\mathrm{a}\neq\mathrm{b}\in\boldsymbol{\mathrm{R}}\right] \\ $$
Answered by TANMAY PANACEA last updated on 28/Oct/20
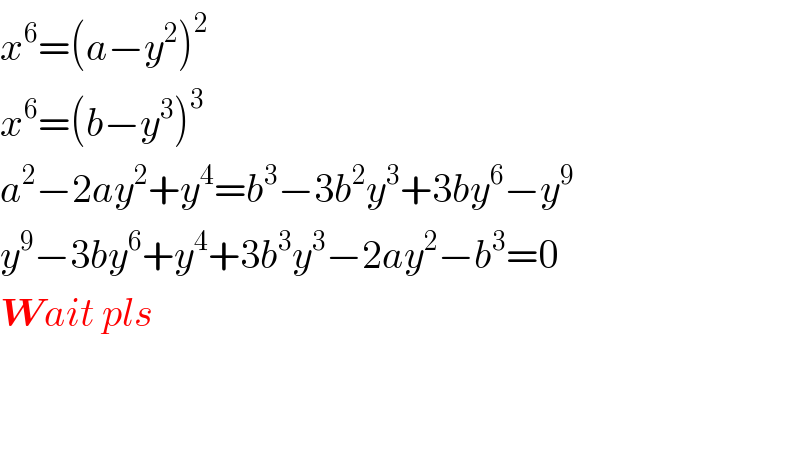
$${x}^{\mathrm{6}} =\left({a}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{6}} =\left({b}−{y}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ay}^{\mathrm{2}} +{y}^{\mathrm{4}} ={b}^{\mathrm{3}} −\mathrm{3}{b}^{\mathrm{2}} {y}^{\mathrm{3}} +\mathrm{3}{by}^{\mathrm{6}} −{y}^{\mathrm{9}} \\ $$$${y}^{\mathrm{9}} −\mathrm{3}{by}^{\mathrm{6}} +{y}^{\mathrm{4}} +\mathrm{3}{b}^{\mathrm{3}} {y}^{\mathrm{3}} −\mathrm{2}{ay}^{\mathrm{2}} −{b}^{\mathrm{3}} =\mathrm{0} \\ $$$$\boldsymbol{{W}}{ait}\:{pls} \\ $$$$ \\ $$$$ \\ $$
