
Question Number 119588 by zakirullah last updated on 25/Oct/20
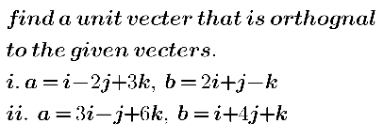
Answered by bemath last updated on 25/Oct/20

$$\left({i}\right)\:{let}\:\overset{\rightarrow} {{c}}\:{is}\:{unit}\:{vector}\:{such}\:{that} \\ $$$${orthogonal}\:{to}\:\overset{\rightarrow} {{a}}\:\&\:\overset{\rightarrow} {{b}} \\ $$$$\:{so}\:{gives}\:\overset{\rightarrow} {{c}}\:=\:\pm\:\frac{\mid\overset{\rightarrow} {{c}}\:\mid\left(\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\right)}{\mid\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:\mid} \\ $$$$\left(\bullet\right)\:\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:=\:\begin{vmatrix}{\mathrm{1}\:\:\:−\mathrm{2}\:\:\:\:\:\:\mathrm{3}}\\{\mathrm{2}\:\:\:\:\:\:\mathrm{1}\:\:\:\:−\mathrm{1}\:\:\:}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(−\mathrm{1},\:\mathrm{7},\:\mathrm{5}\right) \\ $$$${hence}\:\overset{\rightarrow} {{c}}\:=\:\pm\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{49}+\mathrm{25}}}\:\left(−{i}+\mathrm{7}{j}+\mathrm{5}{k}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\pm\:\frac{\mathrm{1}}{\:\mathrm{5}\sqrt{\mathrm{3}}}\:\left(−{i}+\mathrm{7}{j}+\mathrm{5}{k}\:\right) \\ $$$$ \\ $$
Commented by zakirullah last updated on 25/Oct/20

$$\boldsymbol{{thanks}}\:\boldsymbol{{alot}} \\ $$
