
Question Number 119386 by ZiYangLee last updated on 24/Oct/20
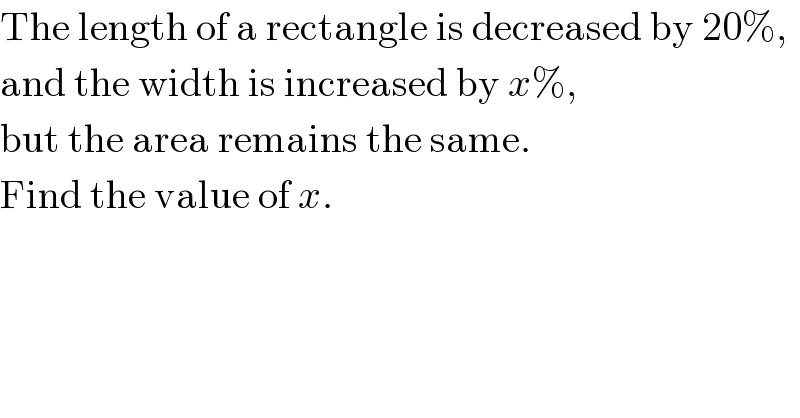
$$\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rectangle}\:\mathrm{is}\:\mathrm{decreased}\:\mathrm{by}\:\mathrm{20\%}, \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{width}\:\mathrm{is}\:\mathrm{increased}\:\mathrm{by}\:{x\%}, \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{area}\:\mathrm{remains}\:\mathrm{the}\:\mathrm{same}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}. \\ $$
Answered by mr W last updated on 24/Oct/20
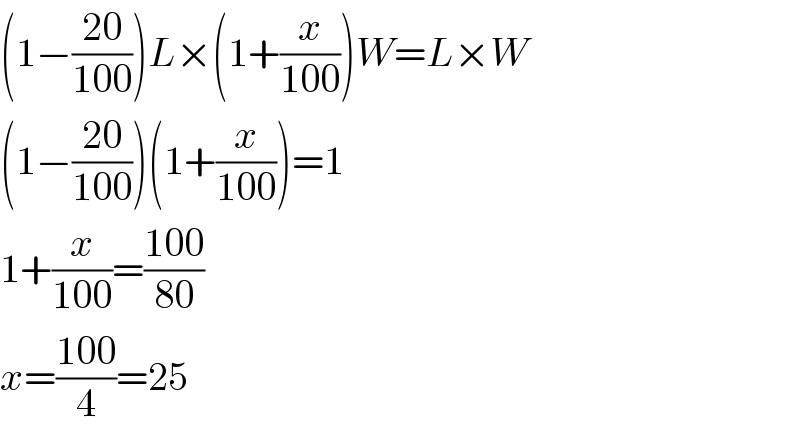
$$\left(\mathrm{1}−\frac{\mathrm{20}}{\mathrm{100}}\right){L}×\left(\mathrm{1}+\frac{{x}}{\mathrm{100}}\right){W}={L}×{W} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{20}}{\mathrm{100}}\right)\left(\mathrm{1}+\frac{{x}}{\mathrm{100}}\right)=\mathrm{1} \\ $$$$\mathrm{1}+\frac{{x}}{\mathrm{100}}=\frac{\mathrm{100}}{\mathrm{80}} \\ $$$${x}=\frac{\mathrm{100}}{\mathrm{4}}=\mathrm{25} \\ $$
Commented by ZiYangLee last updated on 24/Oct/20

$$\bigstar \\ $$
Answered by som(math1967) last updated on 24/Oct/20
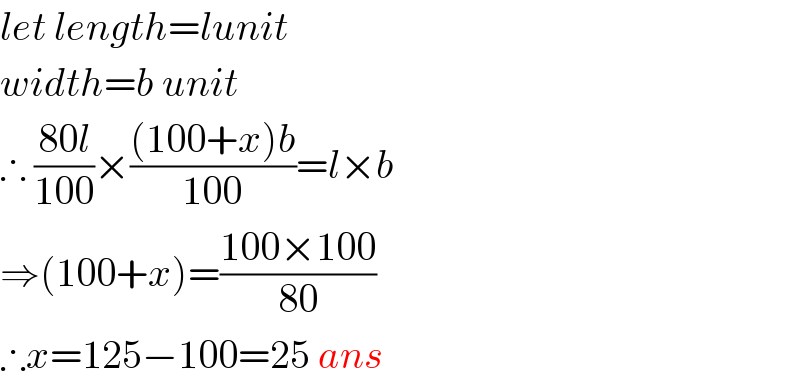
$${let}\:{length}={lunit} \\ $$$${width}={b}\:{unit} \\ $$$$\therefore\:\frac{\mathrm{80}{l}}{\mathrm{100}}×\frac{\left(\mathrm{100}+{x}\right){b}}{\mathrm{100}}={l}×{b} \\ $$$$\Rightarrow\left(\mathrm{100}+{x}\right)=\frac{\mathrm{100}×\mathrm{100}}{\mathrm{80}} \\ $$$$\therefore{x}=\mathrm{125}−\mathrm{100}=\mathrm{25}\:{ans} \\ $$
Commented by ZiYangLee last updated on 24/Oct/20

$$\bigstar \\ $$
