
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 119364 by bobhans last updated on 24/Oct/20

$${Suppose}\:{once}\:{more}\:{we}'{re}\:{asked}\: \\ $$$${to}\:{choose}\:{four}\:{students}\:{from}\:{high}\:{school} \\ $$$${class}\:{of}\:\mathrm{15}\:{to}\:{form}\:{a}\:{committee} \\ $$$${but}\:{this}\:{time}\:{we}\:{have}\:{a}\:{restriction} \\ $$$$:\:{we}\:{don}'{t}\:{want}\:{to}\:{committee}\:{to} \\ $$$${consist}\:{of}\:{all}\:{seniors}\:{or}\:{all}\:{juniors} \\ $$$$.{suppose}\:{there}\:{are}\:{eight}\:{seniors} \\ $$$${and}\:{seven}\:{juniors}\:{in}\:{the}\:{class}.\:{How}\:{many} \\ $$$${different}\:{committe}\:{can}\:{we}\:{form}? \\ $$$$ \\ $$
Answered by john santu last updated on 24/Oct/20

$${This}\:{clearly}\:{call}\:{for}\:{subtraction}\:{principle} \\ $$$${The}\:{total}\:{number}\:{of}\:{possible}\:{committe}\:{is} \\ $$$$\:\:\:\begin{pmatrix}{\mathrm{15}}\\{\:\:\mathrm{4}}\end{pmatrix}\:=\:\frac{\mathrm{15}×\mathrm{14}×\mathrm{13}×\mathrm{12}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}\:=\:\mathrm{1},\mathrm{365} \\ $$$${The}\:{number}\:{of}\:{committe}\:{consisting}\:{all}\:{senior}\:{is} \\ $$$$\:\:\:\begin{pmatrix}{\mathrm{8}}\\{\mathrm{4}}\end{pmatrix}\:=\:\frac{\mathrm{8}×\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}\:=\:\mathrm{70} \\ $$$${and}\:{the}\:{number}\:{of}\:{committe}\:{consisting}\:{all} \\ $$$${juniors}\:{is}\:\begin{pmatrix}{\mathrm{7}}\\{\mathrm{4}}\end{pmatrix}\:=\:\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{4}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}=\:\mathrm{35} \\ $$$${if}\:{we}\:{exlude}\:{those}\:,\:{we}\:{see}\:{that}\:{the}\: \\ $$$${number}\:{of}\:{allowable}\:{committe}\:{is} \\ $$$$\:\mathrm{1},\mathrm{365}−\mathrm{70}−\mathrm{35}\:=\:\mathrm{1},\mathrm{260} \\ $$
Commented by bobhans last updated on 24/Oct/20

$${nice}... \\ $$
Answered by mr W last updated on 24/Oct/20
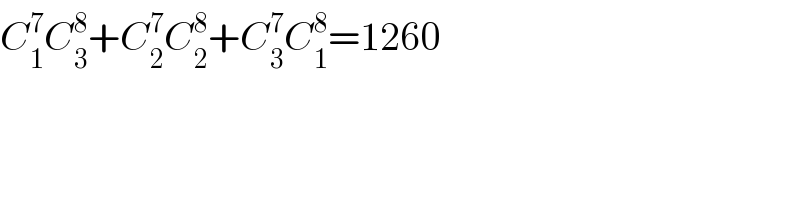
$${C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{3}} ^{\mathrm{8}} +{C}_{\mathrm{2}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{8}} +{C}_{\mathrm{3}} ^{\mathrm{7}} {C}_{\mathrm{1}} ^{\mathrm{8}} =\mathrm{1260} \\ $$
