
Previous in Differential Equation Next in Differential Equation
Question Number 11920 by carrot last updated on 05/Apr/17
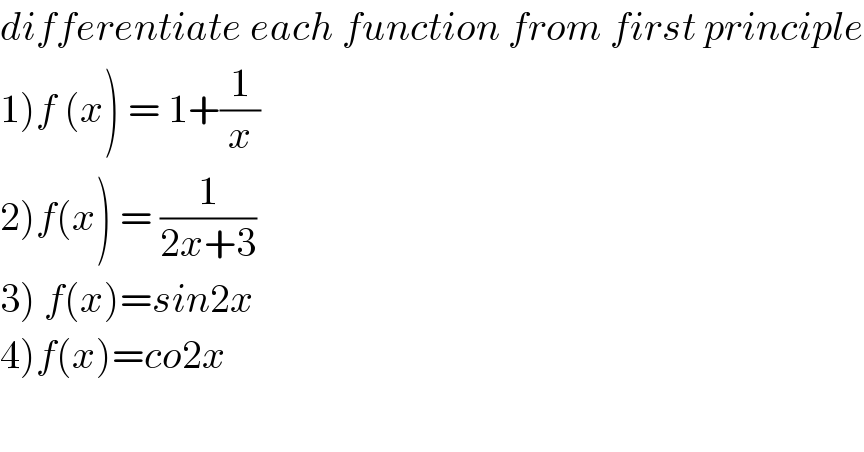
$${differentiate}\:{each}\:{function}\:{from}\:{first}\:{principle} \\ $$$$\left.\mathrm{1}\right){f}\:\left({x}\right)\:=\:\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$$$\left.\mathrm{2}\right){f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\: \\ $$$$\left.\mathrm{3}\right)\:{f}\left({x}\right)={sin}\mathrm{2}{x} \\ $$$$\left.\mathrm{4}\right){f}\left({x}\right)={co}\mathrm{2}{x} \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 05/Apr/17
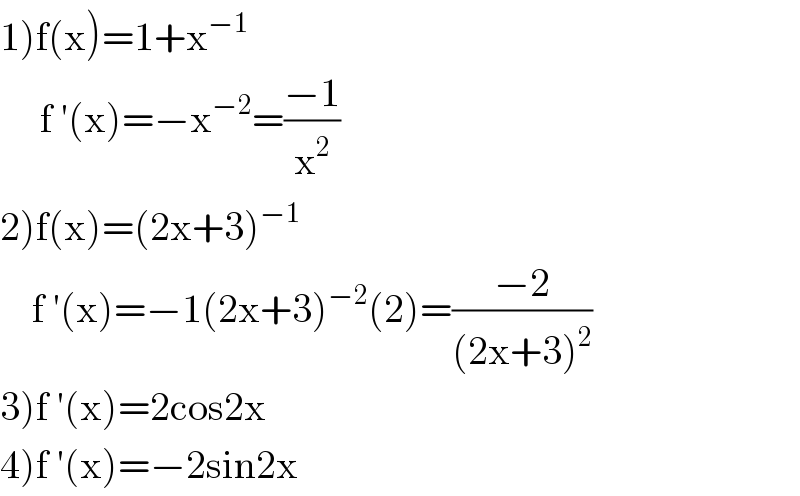
$$\left.\mathrm{1}\right)\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{x}^{−\mathrm{2}} =\frac{−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{2x}+\mathrm{3}\right)^{−\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{1}\left(\mathrm{2x}+\mathrm{3}\right)^{−\mathrm{2}} \left(\mathrm{2}\right)=\frac{−\mathrm{2}}{\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} }\:\:\:\:\:\: \\ $$$$\left.\mathrm{3}\right)\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2cos2x} \\ $$$$\left.\mathrm{4}\right)\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{2sin2x} \\ $$
Commented by carrot last updated on 05/Apr/17
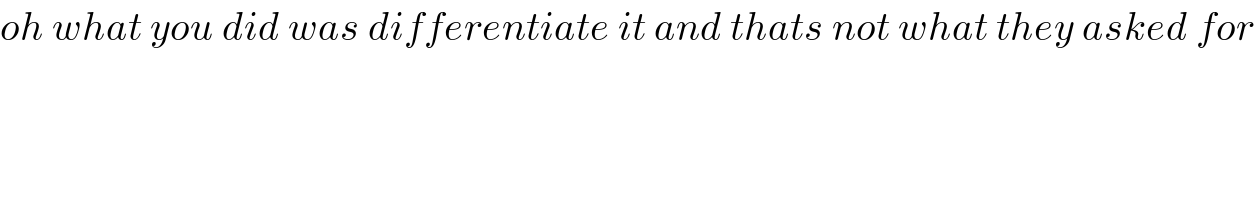
$${oh}\:{what}\:{you}\:{did}\:{was}\:{differentiate}\:{it}\:{and}\:{thats}\:{not}\:{what}\:{they}\:{asked}\:{for} \\ $$
Commented by sandy_suhendra last updated on 06/Apr/17
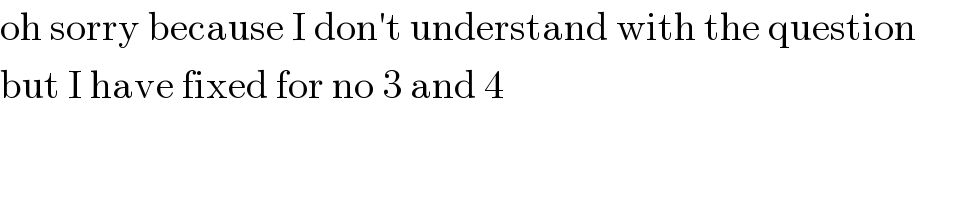
$$\mathrm{oh}\:\mathrm{sorry}\:\mathrm{because}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{with}\:\mathrm{the}\:\mathrm{question}\:\:\:\:\: \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{have}\:\mathrm{fixed}\:\mathrm{for}\:\mathrm{no}\:\mathrm{3}\:\mathrm{and}\:\mathrm{4} \\ $$
Answered by FilupS last updated on 05/Apr/17
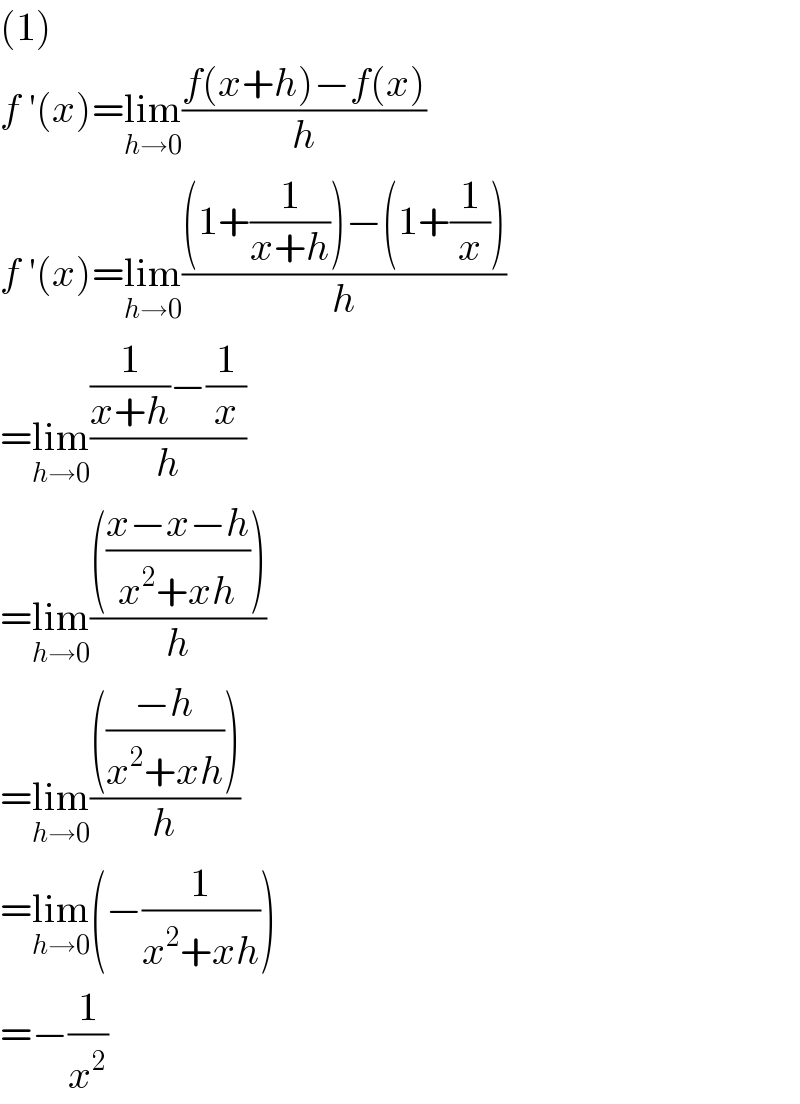
$$\left(\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}+{h}}\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{x}+{h}}−\frac{\mathrm{1}}{{x}}}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{{x}−{x}−{h}}{{x}^{\mathrm{2}} +{xh}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−{h}}{{x}^{\mathrm{2}} +{xh}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{xh}}\right) \\ $$$$=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$
Answered by FilupS last updated on 05/Apr/17
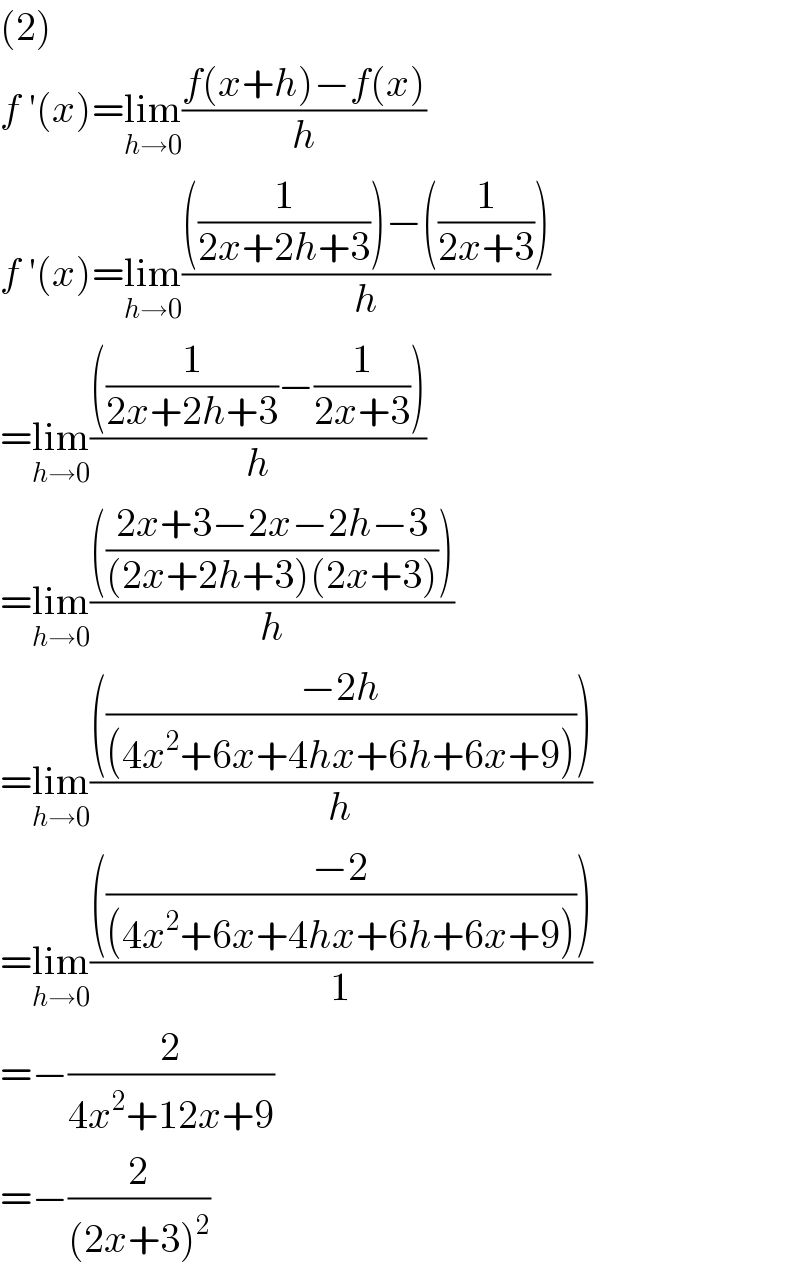
$$\left(\mathrm{2}\right) \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}\right)−\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{2}{x}+\mathrm{3}−\mathrm{2}{x}−\mathrm{2}{h}−\mathrm{3}}{\left(\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−\mathrm{2}{h}}{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}{hx}+\mathrm{6}{h}+\mathrm{6}{x}+\mathrm{9}\right)}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−\mathrm{2}}{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}{hx}+\mathrm{6}{h}+\mathrm{6}{x}+\mathrm{9}\right)}\right)}{\mathrm{1}} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}} \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Answered by sandy_suhendra last updated on 06/Apr/17
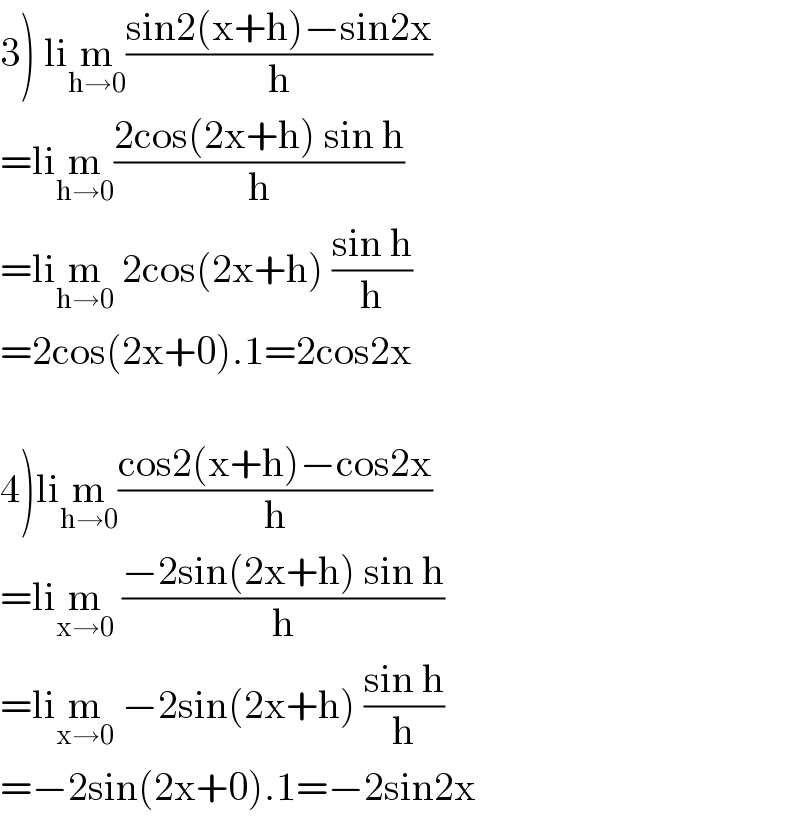
$$\left.\mathrm{3}\right)\:\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{sin2}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{sin2x}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{2cos}\left(\mathrm{2x}+\mathrm{h}\right)\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\:\mathrm{2cos}\left(\mathrm{2x}+\mathrm{h}\right)\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{2cos}\left(\mathrm{2x}+\mathrm{0}\right).\mathrm{1}=\mathrm{2cos2x} \\ $$$$ \\ $$$$\left.\mathrm{4}\right)\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{cos2}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{cos2x}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:\frac{−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{h}\right)\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{h}\right)\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{0}\right).\mathrm{1}=−\mathrm{2sin2x} \\ $$
