
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 119124 by abdullahquwatan last updated on 22/Oct/20
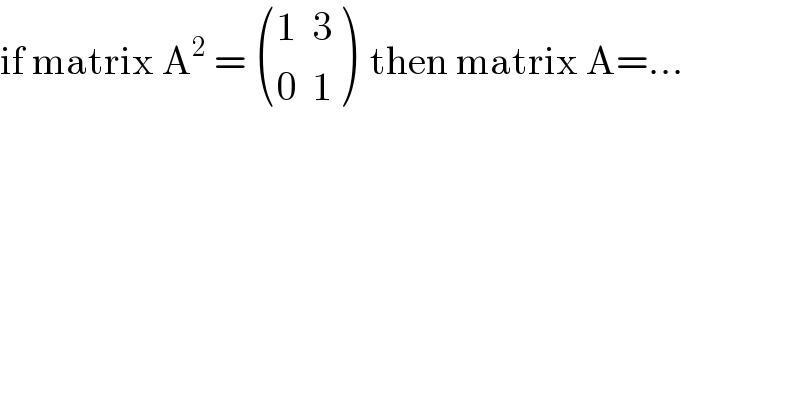
$$\mathrm{if}\:\mathrm{matrix}\:\mathrm{A}^{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{1}\:\:\mathrm{3}}\\{\mathrm{0}\:\:\mathrm{1}}\end{pmatrix}\:\:\mathrm{then}\:\mathrm{matrix}\:\mathrm{A}=... \\ $$
Answered by benjo_mathlover last updated on 22/Oct/20
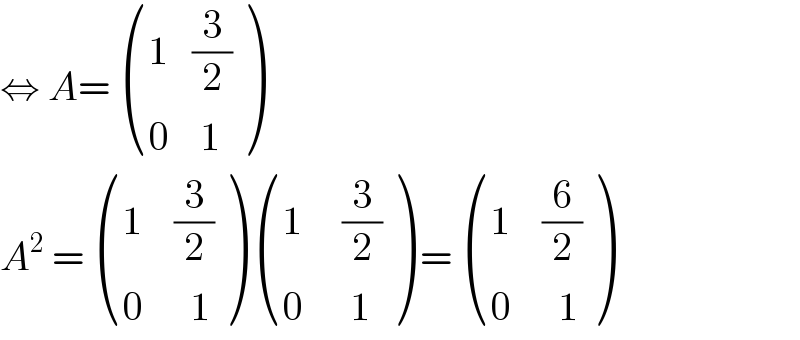
$$\Leftrightarrow\:{A}=\:\begin{pmatrix}{\mathrm{1}\:\:\:\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\frac{\mathrm{6}}{\mathrm{2}}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$
Commented by abdullahquwatan last updated on 22/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mindispower last updated on 23/Oct/20
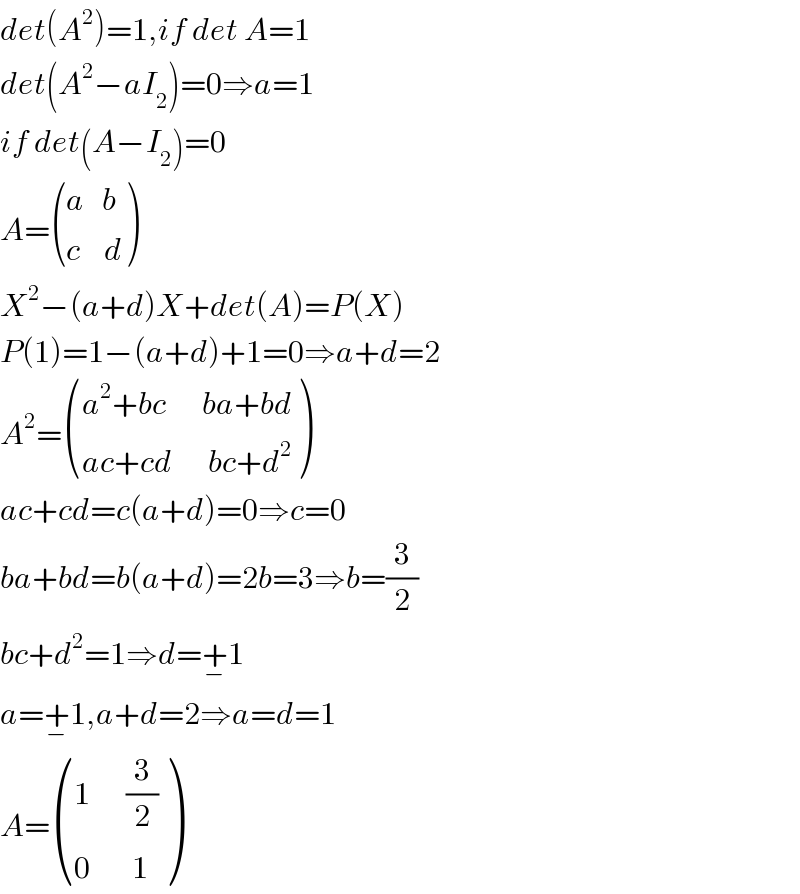
$${det}\left({A}^{\mathrm{2}} \right)=\mathrm{1},{if}\:{det}\:{A}=\mathrm{1} \\ $$$${det}\left({A}^{\mathrm{2}} −{aI}_{\mathrm{2}} \right)=\mathrm{0}\Rightarrow{a}=\mathrm{1} \\ $$$${if}\:{det}\left({A}−{I}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$${A}=\begin{pmatrix}{{a}\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix} \\ $$$${X}^{\mathrm{2}} −\left({a}+{d}\right){X}+{det}\left({A}\right)={P}\left({X}\right) \\ $$$${P}\left(\mathrm{1}\right)=\mathrm{1}−\left({a}+{d}\right)+\mathrm{1}=\mathrm{0}\Rightarrow{a}+{d}=\mathrm{2} \\ $$$${A}^{\mathrm{2}} =\begin{pmatrix}{{a}^{\mathrm{2}} +{bc}\:\:\:\:\:\:{ba}+{bd}}\\{{ac}+{cd}\:\:\:\:\:\:{bc}+{d}^{\mathrm{2}} }\end{pmatrix} \\ $$$${ac}+{cd}={c}\left({a}+{d}\right)=\mathrm{0}\Rightarrow{c}=\mathrm{0} \\ $$$${ba}+{bd}={b}\left({a}+{d}\right)=\mathrm{2}{b}=\mathrm{3}\Rightarrow{b}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${bc}+{d}^{\mathrm{2}} =\mathrm{1}\Rightarrow{d}=\underset{−} {+}\mathrm{1} \\ $$$${a}=\underset{−} {+}\mathrm{1},{a}+{d}=\mathrm{2}\Rightarrow{a}={d}=\mathrm{1} \\ $$$${A}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$
