
Question Number 119070 by benjo_mathlover last updated on 22/Oct/20
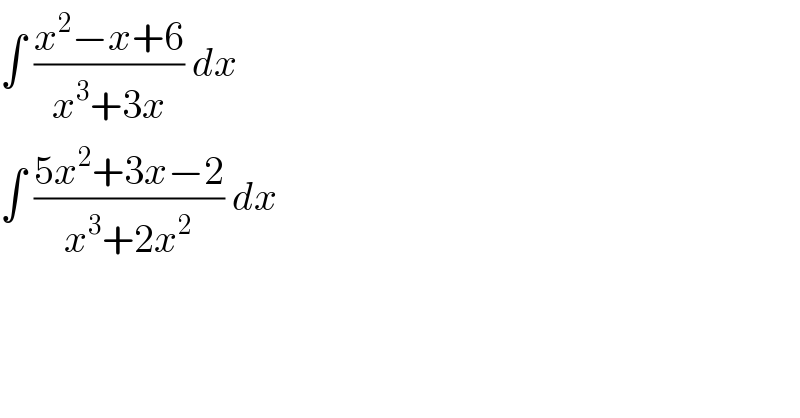
$$\int\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{6}}{{x}^{\mathrm{3}} +\mathrm{3}{x}}\:{dx}\: \\ $$$$\int\:\frac{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}}{{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} }\:{dx}\: \\ $$
Answered by Olaf last updated on 22/Oct/20
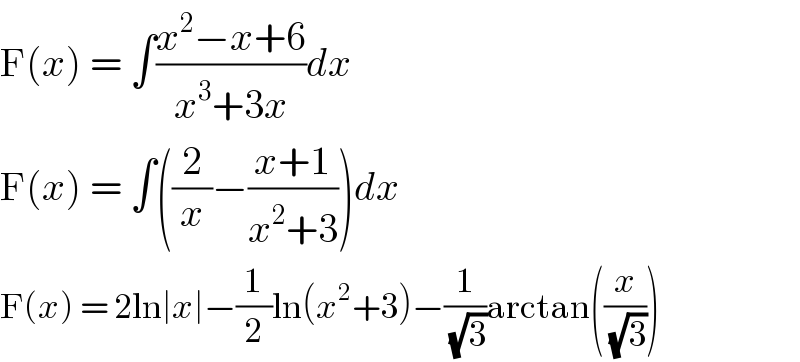
$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{x}^{\mathrm{2}} −{x}+\mathrm{6}}{{x}^{\mathrm{3}} +\mathrm{3}{x}}{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\left(\frac{\mathrm{2}}{{x}}−\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{2ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right) \\ $$
Answered by Olaf last updated on 22/Oct/20
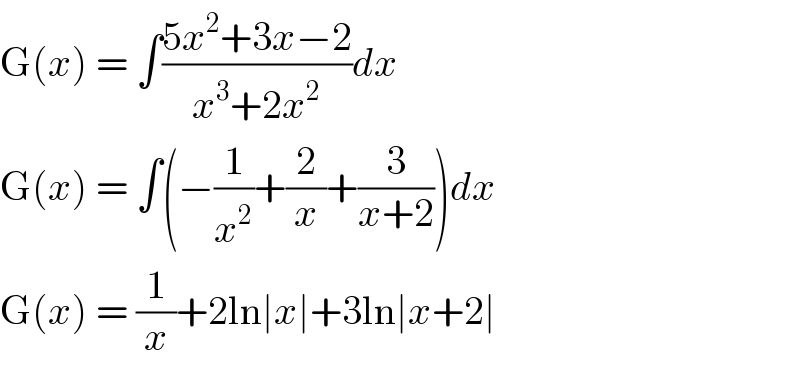
$$\mathrm{G}\left({x}\right)\:=\:\int\frac{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}}{{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{G}\left({x}\right)\:=\:\int\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{{x}}+\frac{\mathrm{3}}{{x}+\mathrm{2}}\right){dx} \\ $$$$\mathrm{G}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}+\mathrm{2ln}\mid{x}\mid+\mathrm{3ln}\mid{x}+\mathrm{2}\mid \\ $$
