
Question Number 118967 by obaidullah last updated on 21/Oct/20
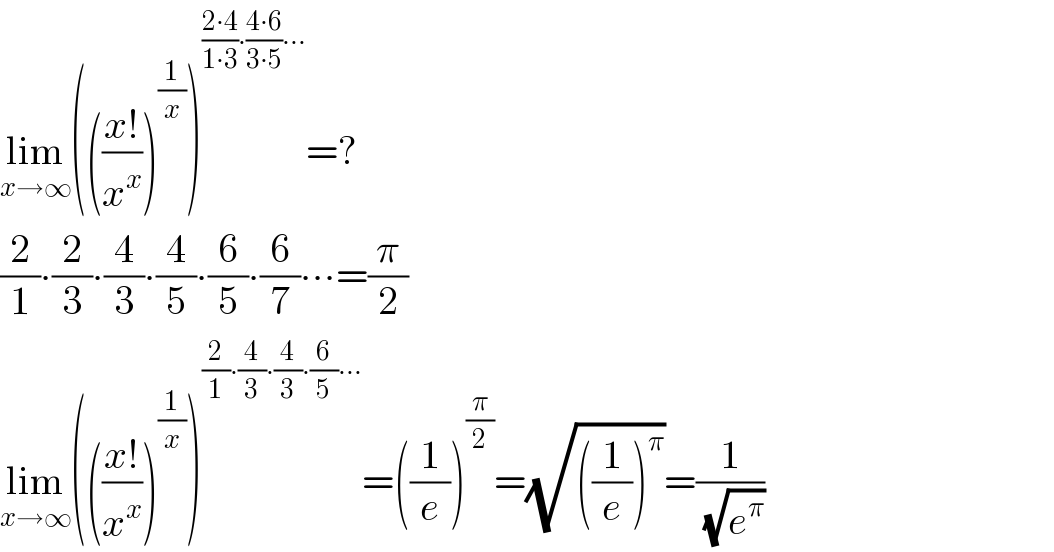
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \right)^{\frac{\mathrm{2}\centerdot\mathrm{4}}{\mathrm{1}\centerdot\mathrm{3}}\centerdot\frac{\mathrm{4}\centerdot\mathrm{6}}{\mathrm{3}\centerdot\mathrm{5}}\centerdot\centerdot\centerdot} =? \\ $$$$\frac{\mathrm{2}}{\mathrm{1}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\mathrm{6}}{\mathrm{5}}\centerdot\frac{\mathrm{6}}{\mathrm{7}}\centerdot\centerdot\centerdot=\frac{\pi}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \right)^{\frac{\mathrm{2}}{\mathrm{1}}\centerdot\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\mathrm{6}}{\mathrm{5}}\centerdot\centerdot\centerdot} =\left(\frac{\mathrm{1}}{{e}}\right)^{\frac{\pi}{\mathrm{2}}} =\sqrt{\left(\frac{\mathrm{1}}{{e}}\right)^{\pi} }=\frac{\mathrm{1}}{\:\sqrt{{e}^{\pi} }} \\ $$
