
Question Number 118811 by ajfour last updated on 19/Oct/20
Commented by ajfour last updated on 19/Oct/20

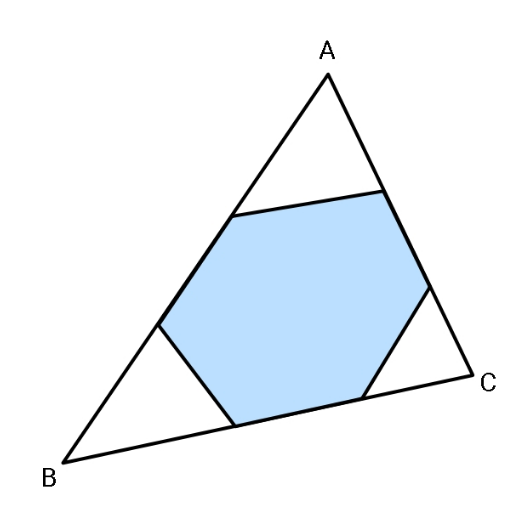
$${What}\:{is}\:{the}\:{side}\:{length}\:{of}\:{the}\:{equal} \\ $$$${sided}\:{hexagon}\:{inscribed}\:{within}\:{the} \\ $$$${triangle}\:{ABC}\:{as}\:{shown}? \\ $$
Commented by I want to learn more last updated on 20/Oct/20
$$\mathrm{MrW},\:\mathrm{please}\:\mathrm{come}\:\mathrm{and}\:\mathrm{solve}.\: \\ $$
Commented by mr W last updated on 21/Oct/20
$${ajfour}\:{sir}: \\ $$$${i}\:{think}\:{there}\:{is}\:{no}\:{unique}\:{solution}. \\ $$
Commented by ajfour last updated on 21/Oct/20
$${fine}\:{sir},\:{how}\:{about}\:{extreme}\:{values}? \\ $$
Answered by 1549442205PVT last updated on 20/Oct/20

$$\mathrm{This}\:\mathrm{problem}\:\mathrm{has}\:\mathrm{infinite}\:\mathrm{many}\:\mathrm{of} \\ $$$$\mathrm{solutions}\:\mathrm{in}\:\mathrm{case}\:\mathrm{the}\:\mathrm{triangle}\:\:\mathrm{ABC}\: \\ $$$$\mathrm{is}\:\mathrm{equilateral}\:\mathrm{since}\:\mathrm{we}\:\mathrm{can}\:\mathrm{construct} \\ $$$$\mathrm{an}\:\mathrm{infinite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{hexagons}\:\mathrm{with} \\ $$$$\mathrm{equal}\:\mathrm{sides}\:\mathrm{and}\:\mathrm{side}\:\mathrm{length}\:\mathrm{is}\:\mathrm{different} \\ $$
Commented by ajfour last updated on 20/Oct/20
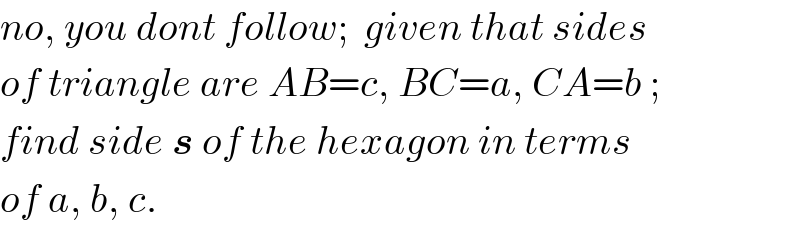
$${no},\:{you}\:{dont}\:{follow};\:\:{given}\:{that}\:{sides} \\ $$$${of}\:{triangle}\:{are}\:{AB}={c},\:{BC}={a},\:{CA}={b}\:; \\ $$$${find}\:{side}\:\boldsymbol{{s}}\:{of}\:{the}\:{hexagon}\:{in}\:{terms} \\ $$$${of}\:{a},\:{b},\:{c}. \\ $$
Commented by 1549442205PVT last updated on 20/Oct/20
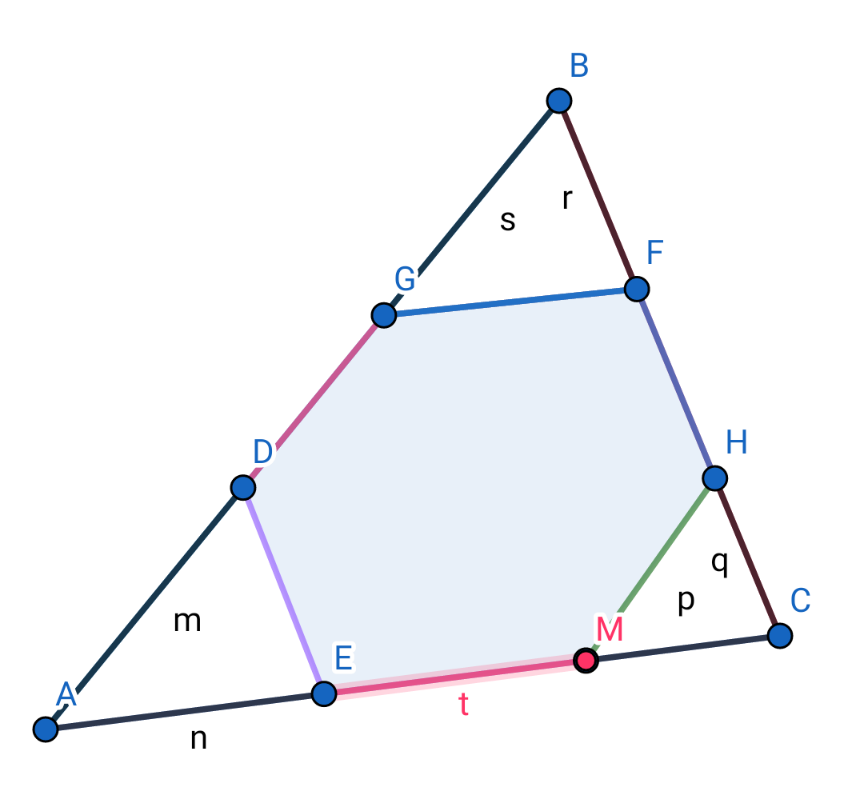
Commented by 1549442205PVT last updated on 20/Oct/20

$$\mathrm{Put}\:\mathrm{AD}=\mathrm{m},\mathrm{AE}=\mathrm{n},\mathrm{CM}=\mathrm{p},\mathrm{CH}=\mathrm{q},\mathrm{ME}=\mathrm{t} \\ $$$$\mathrm{BF}=\mathrm{r},\mathrm{BG}=\mathrm{s},\mathrm{BC}=\mathrm{a},\mathrm{AC}=\mathrm{b},\mathrm{AB}=\mathrm{c} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{have}\:: \\ $$$$\begin{cases}{\mathrm{t}^{\mathrm{2}} =\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} −\mathrm{2mncosA}\left(\mathrm{1}\right)}\\{\mathrm{t}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{2pqcosC}\left(\mathrm{2}\right)}\\{\mathrm{t}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} −\mathrm{2rscosB}\left(\mathrm{3}\right)}\\{\mathrm{n}+\mathrm{t}+\mathrm{p}=\mathrm{b}\left(\mathrm{4}\right)}\\{\mathrm{q}+\mathrm{t}+\mathrm{r}=\mathrm{a}\left(\mathrm{5}\right)}\\{\mathrm{m}+\mathrm{t}+\mathrm{s}=\mathrm{c}\left(\mathrm{6}\right)}\end{cases} \\ $$$$\mathrm{Thus},\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{6}\:\mathrm{equations} \\ $$$$\mathrm{with}\:\mathrm{6}\:\mathrm{unknowns}\:\mathrm{where}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{cosA}, \\ $$$$\mathrm{cosB},\mathrm{cosC}\:\mathrm{are}\:\mathrm{parameters}\:\mathrm{which}\: \\ $$$$\mathrm{are}\:\mathrm{independent}\:\mathrm{together}\:\mathrm{and}\:\mathrm{now} \\ $$$$\mathrm{we}\:\mathrm{need}\:\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}. \\ $$$$ \\ $$
Commented by I want to learn more last updated on 20/Oct/20

$$\mathrm{Sir},\:\mathrm{1549442205PVT}\:\:\mathrm{which}\:\mathrm{app}\:\mathrm{you}\:\mathrm{use}\:\mathrm{to}\:\mathrm{draw}. \\ $$
Commented by 1549442205PVT last updated on 21/Oct/20
$$\mathrm{Geogebra},\mathrm{Drawing}\:\mathrm{of}\:\mathrm{tinkutara}\:\mathrm{done}\:\mathrm{this} \\ $$
Commented by mr W last updated on 21/Oct/20

$$\mathrm{6}\:{equations},\:{but}\:\mathrm{7}\:{unknowns}, \\ $$$${does}\:{it}\:{mean}\:{that}\:{there}\:{is}\:{no}\:{unique} \\ $$$${solution}? \\ $$
Commented by 1549442205PVT last updated on 25/Oct/20
$$\mathrm{Yes},\mathrm{Sir}\:\mathrm{is}\:\mathrm{right}.\mathrm{I}\:\:\mathrm{also}\:\mathrm{have}\:\mathrm{such}\:\mathrm{thinkings} \\ $$
