
Question Number 118781 by Algoritm last updated on 19/Oct/20
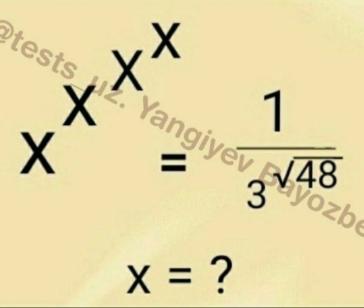
Commented by MJS_new last updated on 19/Oct/20
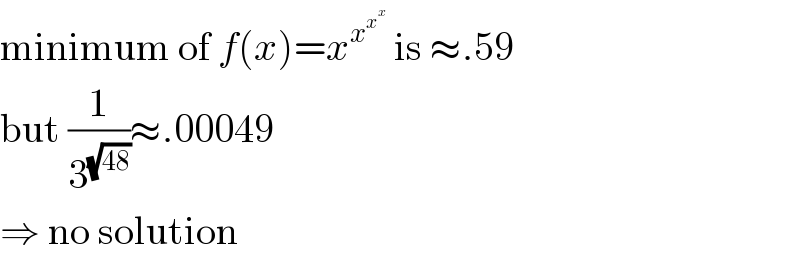
$$\mathrm{minimum}\:\mathrm{of}\:{f}\left({x}\right)={x}^{{x}^{{x}^{{x}} } } \:\mathrm{is}\:\approx.\mathrm{59} \\ $$$$\mathrm{but}\:\frac{\mathrm{1}}{\mathrm{3}^{\sqrt{\mathrm{48}}} }\approx.\mathrm{00049} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$
Commented by Algoritm last updated on 20/Oct/20
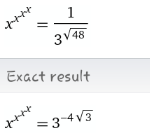
Commented by MJS_new last updated on 20/Oct/20
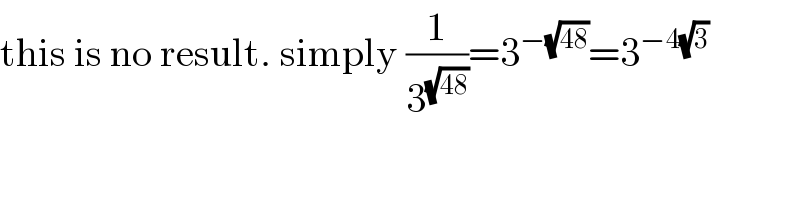
$$\mathrm{this}\:\mathrm{is}\:\mathrm{no}\:\mathrm{result}.\:\mathrm{simply}\:\frac{\mathrm{1}}{\mathrm{3}^{\sqrt{\mathrm{48}}} }=\mathrm{3}^{−\sqrt{\mathrm{48}}} =\mathrm{3}^{−\mathrm{4}\sqrt{\mathrm{3}}} \\ $$
Commented by Algoritm last updated on 20/Oct/20
Commented by MJS_new last updated on 20/Oct/20
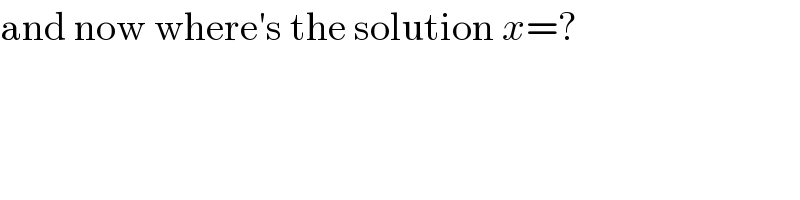
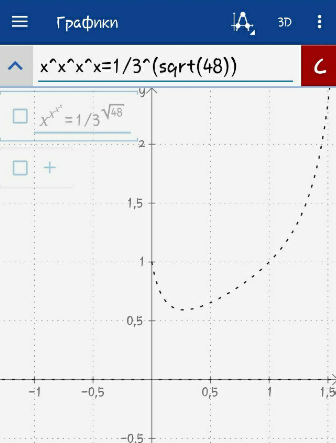
$$\mathrm{and}\:\mathrm{now}\:\mathrm{where}'\mathrm{s}\:\mathrm{the}\:\mathrm{solution}\:{x}=? \\ $$
Commented by MJS_new last updated on 20/Oct/20
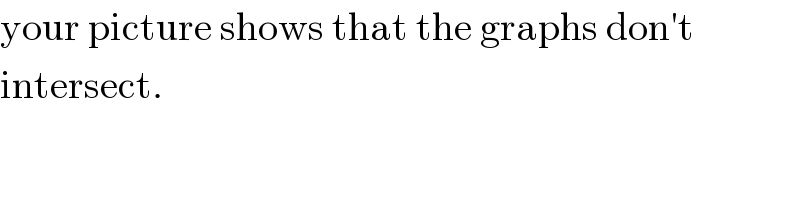
$$\mathrm{your}\:\mathrm{picture}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{graphs}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{intersect}. \\ $$
