
Question Number 118651 by Sherjon last updated on 18/Oct/20

Commented by Sherjon last updated on 18/Oct/20

$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +...=?\:\:\:{Why} \\ $$
Commented by bramlexs22 last updated on 19/Oct/20
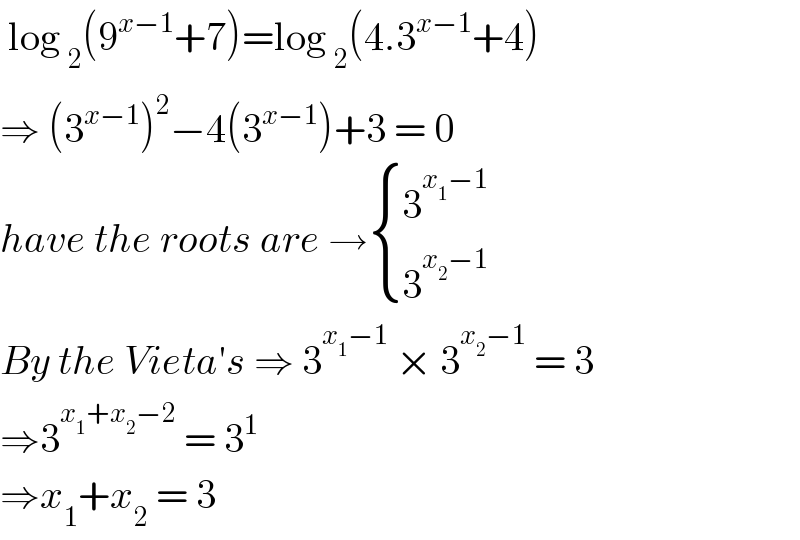
$$\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{9}^{{x}−\mathrm{1}} +\mathrm{7}\right)=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{4}.\mathrm{3}^{{x}−\mathrm{1}} +\mathrm{4}\right) \\ $$$$\Rightarrow\:\left(\mathrm{3}^{{x}−\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{3}^{{x}−\mathrm{1}} \right)+\mathrm{3}\:=\:\mathrm{0}\: \\ $$$${have}\:{the}\:{roots}\:{are}\:\rightarrow\begin{cases}{\mathrm{3}^{{x}_{\mathrm{1}} −\mathrm{1}} }\\{\mathrm{3}^{{x}_{\mathrm{2}} −\mathrm{1}} }\end{cases} \\ $$$${By}\:{the}\:{Vieta}'{s}\:\Rightarrow\:\mathrm{3}^{{x}_{\mathrm{1}} −\mathrm{1}} \:×\:\mathrm{3}^{{x}_{\mathrm{2}} −\mathrm{1}} \:=\:\mathrm{3} \\ $$$$\Rightarrow\mathrm{3}^{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} −\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{1}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} +{x}_{\mathrm{2}} \:=\:\mathrm{3}\: \\ $$
Answered by Dwaipayan Shikari last updated on 18/Oct/20
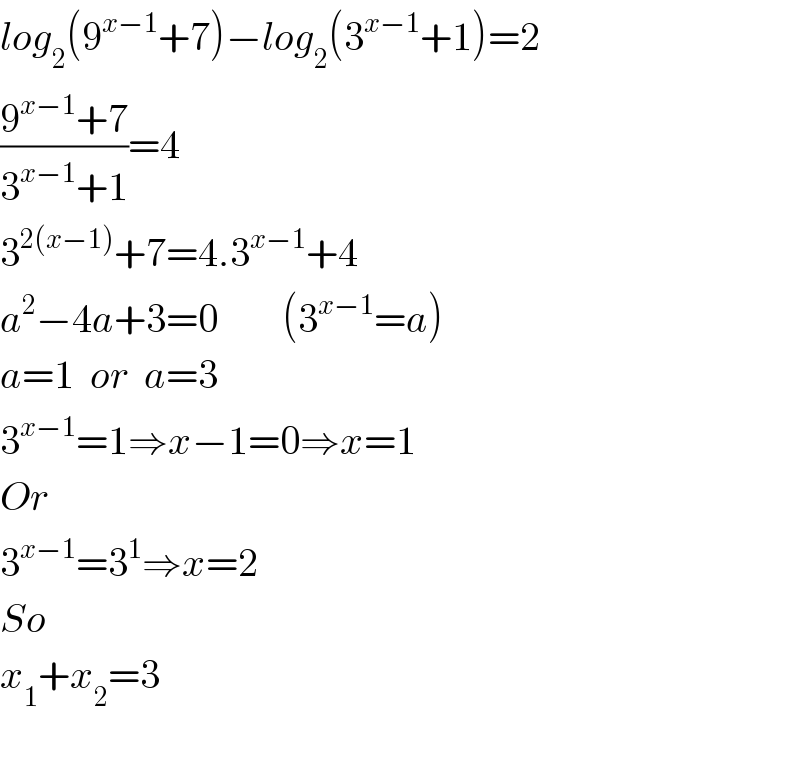
$${log}_{\mathrm{2}} \left(\mathrm{9}^{{x}−\mathrm{1}} +\mathrm{7}\right)−{log}_{\mathrm{2}} \left(\mathrm{3}^{{x}−\mathrm{1}} +\mathrm{1}\right)=\mathrm{2} \\ $$$$\frac{\mathrm{9}^{{x}−\mathrm{1}} +\mathrm{7}}{\mathrm{3}^{{x}−\mathrm{1}} +\mathrm{1}}=\mathrm{4} \\ $$$$\mathrm{3}^{\mathrm{2}\left({x}−\mathrm{1}\right)} +\mathrm{7}=\mathrm{4}.\mathrm{3}^{{x}−\mathrm{1}} +\mathrm{4} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{3}=\mathrm{0}\:\:\:\:\:\:\:\:\left(\mathrm{3}^{{x}−\mathrm{1}} ={a}\right) \\ $$$${a}=\mathrm{1}\:\:{or}\:\:{a}=\mathrm{3} \\ $$$$\mathrm{3}^{{x}−\mathrm{1}} =\mathrm{1}\Rightarrow{x}−\mathrm{1}=\mathrm{0}\Rightarrow{x}=\mathrm{1} \\ $$$${Or} \\ $$$$\mathrm{3}^{{x}−\mathrm{1}} =\mathrm{3}^{\mathrm{1}} \Rightarrow{x}=\mathrm{2} \\ $$$${So} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{3} \\ $$$$ \\ $$
