
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 118640 by 281981 last updated on 18/Oct/20

Answered by MJS_new last updated on 19/Oct/20
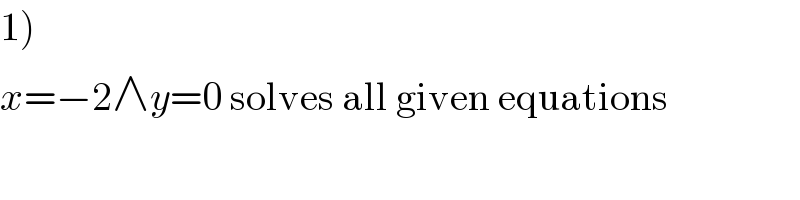
$$\left.\mathrm{1}\right) \\ $$$${x}=−\mathrm{2}\wedge{y}=\mathrm{0}\:\mathrm{solves}\:\mathrm{all}\:\mathrm{given}\:\mathrm{equations} \\ $$
Answered by 1549442205PVT last updated on 19/Oct/20

$$\begin{cases}{\mathrm{2x}+\mathrm{3y}+\mathrm{4}=\mathrm{0}\:\left(\mathrm{1}\right)}\\{\mathrm{3x}+\mathrm{4y}+\mathrm{6}=\mathrm{0}\:\left(\mathrm{2}\right)}\\{\mathrm{4x}+\mathrm{5y}+\mathrm{8}=\mathrm{0}\:\left(\mathrm{3}\right)}\end{cases} \\ $$$$\mathrm{Substracting}\:\left(\mathrm{2}\right)\mathrm{from}\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{2}=\mathrm{0}\left(\mathrm{4}\right)\Leftrightarrow\mathrm{2x}+\mathrm{2y}+\mathrm{4}=\mathrm{0}.\mathrm{Substract} \\ $$$$\mathrm{this}\:\mathrm{equation}\:\mathrm{from}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{y}=\mathrm{0}, \\ $$$$\mathrm{replace}\:\mathrm{into}\:\left(\mathrm{4}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}=−\mathrm{2} \\ $$$$\mathrm{Simce}\:\mathrm{the}\:\mathrm{equations}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\left(\mathrm{3}\right)\:\mathrm{obtained} \\ $$$$\mathrm{from}\:\left(\mathrm{4}\right)\mathrm{by}\:\mathrm{multiplying}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{by} \\ $$$$\mathrm{2},\mathrm{3},\mathrm{4}\:\mathrm{respectively},\mathrm{so}\:\left(\mathrm{x},\mathrm{y}\right)=\left(−\mathrm{2},\mathrm{0}\right)\mathrm{is} \\ $$$$\mathrm{unique}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{system}.\mathrm{Hence} \\ $$$$\left.\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{choose}}\:\boldsymbol{\mathrm{assert}}\:\mathrm{1}\right)\: \\ $$
