
Question Number 118636 by Algoritm last updated on 18/Oct/20
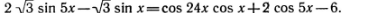
Commented by TANMAY PANACEA last updated on 18/Oct/20
$${what}\:{is}\:{the}\:{question} \\ $$
Commented by Algoritm last updated on 18/Oct/20

$$\mathrm{x}=? \\ $$
Answered by MJS_new last updated on 19/Oct/20
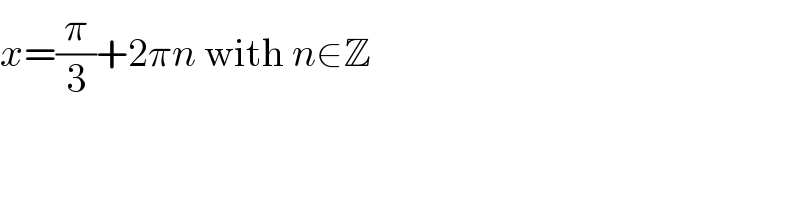
$${x}=\frac{\pi}{\mathrm{3}}+\mathrm{2}\pi{n}\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$
Commented by Algoritm last updated on 19/Oct/20
$$\mathrm{solution}\:\mathrm{sir}\:\mathrm{please} \\ $$
Commented by MJS_new last updated on 19/Oct/20
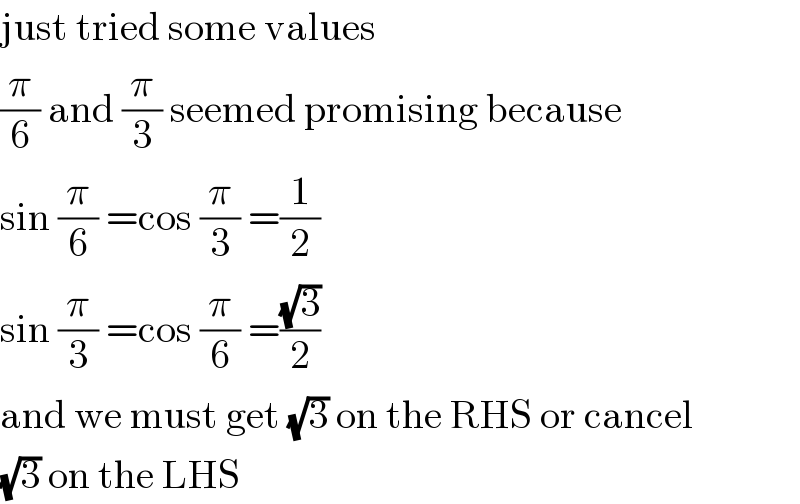
$$\mathrm{just}\:\mathrm{tried}\:\mathrm{some}\:\mathrm{values} \\ $$$$\frac{\pi}{\mathrm{6}}\:\mathrm{and}\:\frac{\pi}{\mathrm{3}}\:\mathrm{seemed}\:\mathrm{promising}\:\mathrm{because} \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\:=\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{must}\:\mathrm{get}\:\sqrt{\mathrm{3}}\:\mathrm{on}\:\mathrm{the}\:\mathrm{RHS}\:\mathrm{or}\:\mathrm{cancel} \\ $$$$\sqrt{\mathrm{3}}\:\mathrm{on}\:\mathrm{the}\:\mathrm{LHS} \\ $$
