
Question Number 118627 by mohammad17 last updated on 18/Oct/20
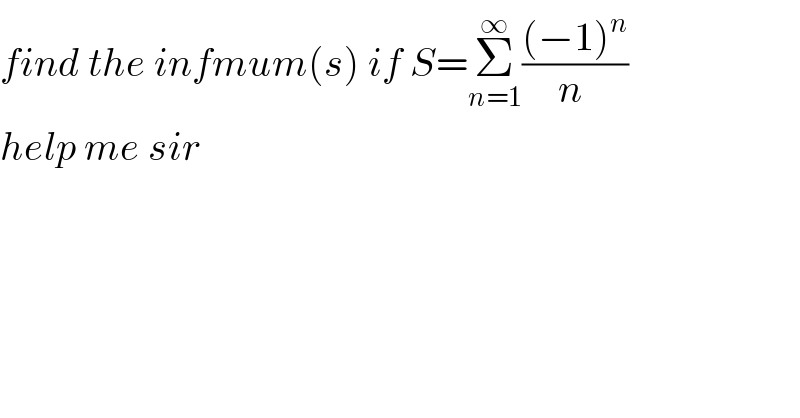
$${find}\:{the}\:{infmum}\left({s}\right)\:{if}\:{S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\:}\: \\ $$$${help}\:{me}\:{sir} \\ $$
Answered by TANMAY PANACEA last updated on 18/Oct/20
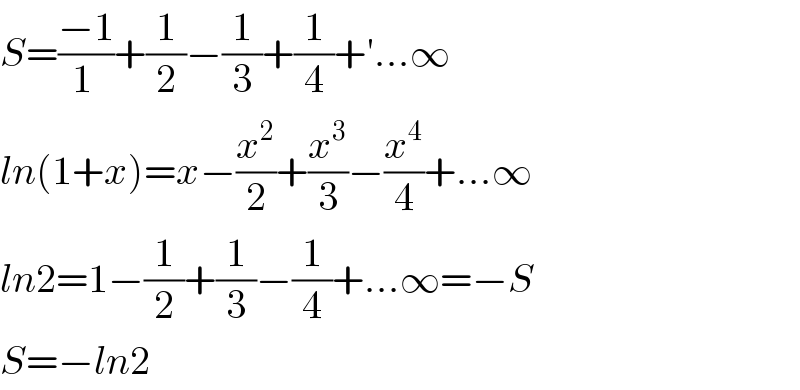
$${S}=\frac{−\mathrm{1}}{\mathrm{1}\:}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+'...\infty \\ $$$${ln}\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+...\infty \\ $$$${ln}\mathrm{2}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+...\infty=−{S} \\ $$$${S}=−{ln}\mathrm{2} \\ $$
