
Question Number 118511 by ZiYangLee last updated on 18/Oct/20
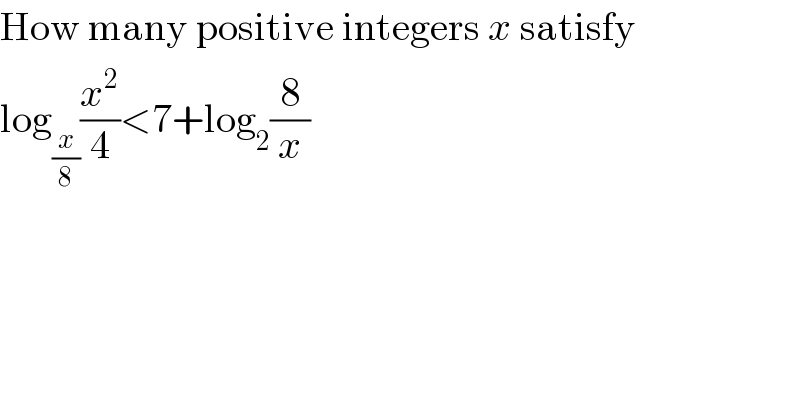
$$\mathrm{How}\:\mathrm{many}\:\mathrm{positive}\:\mathrm{integers}\:{x}\:\mathrm{satisfy} \\ $$ $$\mathrm{log}_{\frac{{x}}{\mathrm{8}}} \frac{{x}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{7}+\mathrm{log}_{\mathrm{2}} \frac{\mathrm{8}}{{x}} \\ $$
Answered by mr W last updated on 18/Oct/20
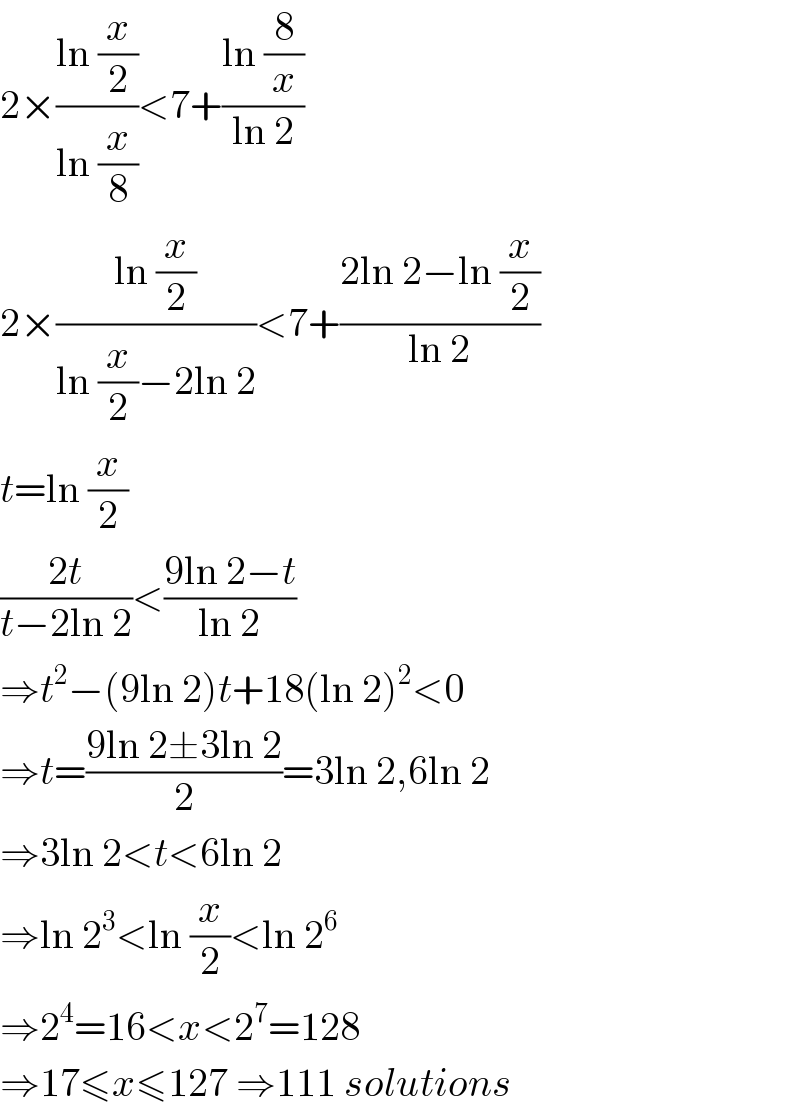
$$\mathrm{2}×\frac{\mathrm{ln}\:\frac{{x}}{\mathrm{2}}}{\mathrm{ln}\:\frac{{x}}{\mathrm{8}}}<\mathrm{7}+\frac{\mathrm{ln}\:\frac{\mathrm{8}}{{x}}}{\mathrm{ln}\:\mathrm{2}} \\ $$ $$\mathrm{2}×\frac{\mathrm{ln}\:\frac{{x}}{\mathrm{2}}}{\mathrm{ln}\:\frac{{x}}{\mathrm{2}}−\mathrm{2ln}\:\mathrm{2}}<\mathrm{7}+\frac{\mathrm{2ln}\:\mathrm{2}−\mathrm{ln}\:\frac{{x}}{\mathrm{2}}}{\mathrm{ln}\:\mathrm{2}} \\ $$ $${t}=\mathrm{ln}\:\frac{{x}}{\mathrm{2}} \\ $$ $$\frac{\mathrm{2}{t}}{{t}−\mathrm{2ln}\:\mathrm{2}}<\frac{\mathrm{9ln}\:\mathrm{2}−{t}}{\mathrm{ln}\:\mathrm{2}} \\ $$ $$\Rightarrow{t}^{\mathrm{2}} −\left(\mathrm{9ln}\:\mathrm{2}\right){t}+\mathrm{18}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} <\mathrm{0} \\ $$ $$\Rightarrow{t}=\frac{\mathrm{9ln}\:\mathrm{2}\pm\mathrm{3ln}\:\mathrm{2}}{\mathrm{2}}=\mathrm{3ln}\:\mathrm{2},\mathrm{6ln}\:\mathrm{2} \\ $$ $$\Rightarrow\mathrm{3ln}\:\mathrm{2}<{t}<\mathrm{6ln}\:\mathrm{2} \\ $$ $$\Rightarrow\mathrm{ln}\:\mathrm{2}^{\mathrm{3}} <\mathrm{ln}\:\frac{{x}}{\mathrm{2}}<\mathrm{ln}\:\mathrm{2}^{\mathrm{6}} \\ $$ $$\Rightarrow\mathrm{2}^{\mathrm{4}} =\mathrm{16}<{x}<\mathrm{2}^{\mathrm{7}} =\mathrm{128} \\ $$ $$\Rightarrow\mathrm{17}\leqslant{x}\leqslant\mathrm{127}\:\Rightarrow\mathrm{111}\:{solutions} \\ $$
Answered by Lordose last updated on 18/Oct/20
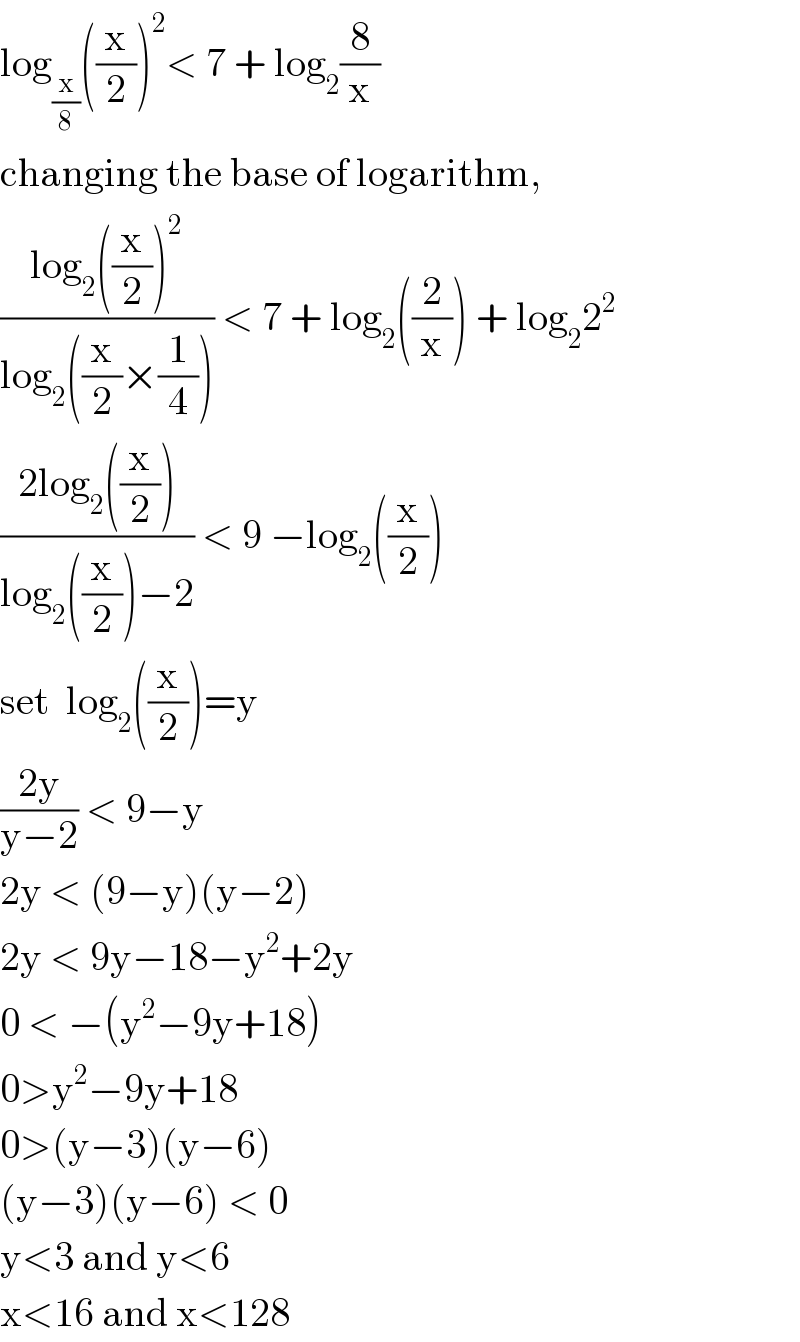
$$\mathrm{log}_{\frac{\mathrm{x}}{\mathrm{8}}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} <\:\mathrm{7}\:+\:\mathrm{log}_{\mathrm{2}} \frac{\mathrm{8}}{\mathrm{x}} \\ $$ $$\mathrm{changing}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{logarithm}, \\ $$ $$\frac{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{4}}\right)}\:<\:\mathrm{7}\:+\:\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)\:+\:\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} \\ $$ $$\frac{\mathrm{2log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}}\:<\:\mathrm{9}\:−\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$ $$\mathrm{set}\:\:\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{y} \\ $$ $$\frac{\mathrm{2y}}{\mathrm{y}−\mathrm{2}}\:<\:\mathrm{9}−\mathrm{y} \\ $$ $$\mathrm{2y}\:<\:\left(\mathrm{9}−\mathrm{y}\right)\left(\mathrm{y}−\mathrm{2}\right) \\ $$ $$\mathrm{2y}\:<\:\mathrm{9y}−\mathrm{18}−\mathrm{y}^{\mathrm{2}} +\mathrm{2y} \\ $$ $$\mathrm{0}\:<\:−\left(\mathrm{y}^{\mathrm{2}} −\mathrm{9y}+\mathrm{18}\right) \\ $$ $$\mathrm{0}>\mathrm{y}^{\mathrm{2}} −\mathrm{9y}+\mathrm{18} \\ $$ $$\mathrm{0}>\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{6}\right) \\ $$ $$\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{6}\right)\:<\:\mathrm{0} \\ $$ $$\mathrm{y}<\mathrm{3}\:\mathrm{and}\:\mathrm{y}<\mathrm{6} \\ $$ $$\mathrm{x}<\mathrm{16}\:\mathrm{and}\:\mathrm{x}<\mathrm{128} \\ $$
Answered by 1549442205PVT last updated on 18/Oct/20
![We need the condition x>0,x≠8 log_(x/8) (x^2 /4)<7+log_2 (8/x)⇔log_(x/8) [((x/8))^2 .16] <7+log_2 8−log_2 x⇔log_(x/8) ((x/8))^2 +log_(x/8) 16 <7+3−log_2 x⇔2+4log_(x/8) 2<10−log_2 x ⇔(4/(log_2 (x/8)))<8−log_2 x⇔(4/(log_2 x−3))<8−log_2 x ⇔(4/(log_2 x−3))+log_2 x−8<0.Put log_2 x=t ⇔(4/(t−3))+t−8<0⇔((t^2 −11t+28)/(t−3))<0 ⇔(((t−4)(t−7))/(t−3))<0 ⇔t∈(−∞,3)∪(4,7) i)log_2 x<3⇔0<x<8 ii)4<log_2 x<7⇔2^4 <x<2^7 ⇔16<x<128 Thus,the roots of given inequality are: x∈(0,8)∪(16,128) Since x∈N^∗ ,x∈{1,2,...,7}∪{17,...,127} hence all there are 11 positive integers satisfying the given inequality](Q118536.png)
$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{x}>\mathrm{0},\mathrm{x}\neq\mathrm{8} \\ $$ $$\mathrm{log}_{\frac{{x}}{\mathrm{8}}} \frac{{x}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{7}+\mathrm{log}_{\mathrm{2}} \frac{\mathrm{8}}{{x}}\Leftrightarrow\mathrm{log}_{\frac{\mathrm{x}}{\mathrm{8}}} \left[\left(\frac{\mathrm{x}}{\mathrm{8}}\right)^{\mathrm{2}} .\mathrm{16}\right] \\ $$ $$<\mathrm{7}+\mathrm{log}_{\mathrm{2}} \mathrm{8}−\mathrm{log}_{\mathrm{2}} \mathrm{x}\Leftrightarrow\mathrm{log}_{\frac{\mathrm{x}}{\mathrm{8}}} \left(\frac{\mathrm{x}}{\mathrm{8}}\right)^{\mathrm{2}} +\mathrm{log}_{\frac{\mathrm{x}}{\mathrm{8}}} \mathrm{16} \\ $$ $$<\mathrm{7}+\mathrm{3}−\mathrm{log}_{\mathrm{2}} \mathrm{x}\Leftrightarrow\mathrm{2}+\mathrm{4log}_{\frac{\mathrm{x}}{\mathrm{8}}} \mathrm{2}<\mathrm{10}−\mathrm{log}_{\mathrm{2}} \mathrm{x} \\ $$ $$\Leftrightarrow\frac{\mathrm{4}}{\mathrm{log}_{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{8}}}<\mathrm{8}−\mathrm{log}_{\mathrm{2}} \mathrm{x}\Leftrightarrow\frac{\mathrm{4}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}−\mathrm{3}}<\mathrm{8}−\mathrm{log}_{\mathrm{2}} \mathrm{x} \\ $$ $$\Leftrightarrow\frac{\mathrm{4}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}−\mathrm{3}}+\mathrm{log}_{\mathrm{2}} \mathrm{x}−\mathrm{8}<\mathrm{0}.\mathrm{Put}\:\mathrm{log}_{\mathrm{2}} \mathrm{x}=\mathrm{t} \\ $$ $$\Leftrightarrow\frac{\mathrm{4}}{\mathrm{t}−\mathrm{3}}+\mathrm{t}−\mathrm{8}<\mathrm{0}\Leftrightarrow\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{11t}+\mathrm{28}}{\mathrm{t}−\mathrm{3}}<\mathrm{0} \\ $$ $$\Leftrightarrow\frac{\left(\mathrm{t}−\mathrm{4}\right)\left(\mathrm{t}−\mathrm{7}\right)}{\mathrm{t}−\mathrm{3}}<\mathrm{0} \\ $$ $$\Leftrightarrow\mathrm{t}\in\left(−\infty,\mathrm{3}\right)\cup\left(\mathrm{4},\mathrm{7}\right) \\ $$ $$\left.\mathrm{i}\right)\mathrm{log}_{\mathrm{2}} \mathrm{x}<\mathrm{3}\Leftrightarrow\mathrm{0}<\mathrm{x}<\mathrm{8} \\ $$ $$\left.\mathrm{ii}\right)\mathrm{4}<\mathrm{log}_{\mathrm{2}} \mathrm{x}<\mathrm{7}\Leftrightarrow\mathrm{2}^{\mathrm{4}} <\mathrm{x}<\mathrm{2}^{\mathrm{7}} \Leftrightarrow\mathrm{16}<\mathrm{x}<\mathrm{128} \\ $$ $$\mathrm{Thus},\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{are}: \\ $$ $$\mathrm{x}\in\left(\mathrm{0},\mathrm{8}\right)\cup\left(\mathrm{16},\mathrm{128}\right) \\ $$ $$\boldsymbol{\mathrm{Since}}\:\boldsymbol{\mathrm{x}}\in\boldsymbol{\mathrm{N}}^{\ast} ,\boldsymbol{\mathrm{x}}\in\left\{\mathrm{1},\mathrm{2},...,\mathrm{7}\right\}\cup\left\{\mathrm{17},...,\mathrm{127}\right\}\: \\ $$ $$\boldsymbol{\mathrm{hence}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{there}}\:\boldsymbol{\mathrm{are}}\:\mathrm{11} \:\boldsymbol{\mathrm{positive}}\:\boldsymbol{\mathrm{integers}} \\ $$ $$\boldsymbol{\mathrm{satisfying}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{inequality}} \\ $$
Commented bymr W last updated on 18/Oct/20

$${very}\:{correct}! \\ $$
Commented by1549442205PVT last updated on 18/Oct/20

$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Commented byZiYangLee last updated on 19/Oct/20

$$\mathrm{PERFECT}!\bigstar\bigstar \\ $$
