
Question Number 118411 by bramlexs22 last updated on 17/Oct/20
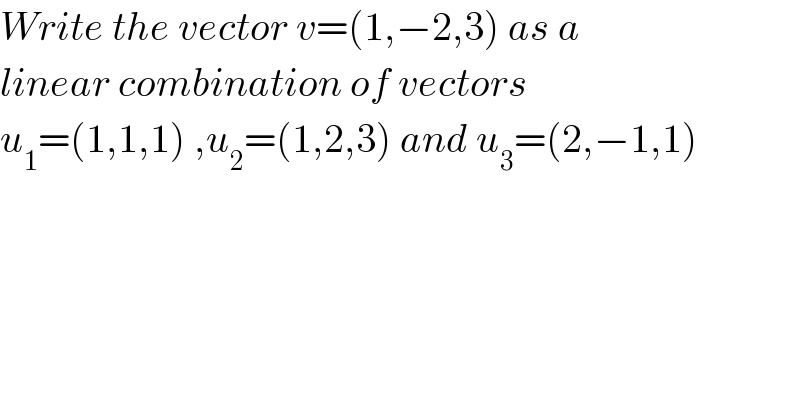
$${Write}\:{the}\:{vector}\:{v}=\left(\mathrm{1},−\mathrm{2},\mathrm{3}\right)\:{as}\:{a} \\ $$$${linear}\:{combination}\:{of}\:{vectors} \\ $$$${u}_{\mathrm{1}} =\left(\mathrm{1},\mathrm{1},\mathrm{1}\right)\:,{u}_{\mathrm{2}} =\left(\mathrm{1},\mathrm{2},\mathrm{3}\right)\:{and}\:{u}_{\mathrm{3}} =\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right) \\ $$
Answered by benjo_mathlover last updated on 17/Oct/20

$${linear}\:{combination}\:{of}\:{vectors} \\ $$$${u}_{\mathrm{1}} ,{u}_{\mathrm{2}} \:{and}\:{u}_{\mathrm{3}} \:,\:{so}\:{v}\:=\:{pu}_{\mathrm{1}} +{qu}_{\mathrm{2}} +{ru}_{\mathrm{3}} \\ $$$$\begin{pmatrix}{\:\:\:\:\mathrm{1}}\\{−\mathrm{2}}\\{\:\:\:\:\mathrm{3}}\end{pmatrix}\:=\:\begin{pmatrix}{{p}}\\{{p}}\\{{p}}\end{pmatrix}\:+\:\begin{pmatrix}{\:\:{q}}\\{\mathrm{2}{q}}\\{\mathrm{3}{q}}\end{pmatrix}\:+\:\begin{pmatrix}{\:\:\mathrm{2}{r}}\\{−{r}}\\{\:\:\:{r}}\end{pmatrix} \\ $$$$\begin{cases}{{p}+{q}+\mathrm{2}{r}\:=\:\mathrm{1}}\\{{p}+\mathrm{2}{q}−{r}\:=\:−\mathrm{2}}\\{{p}+\mathrm{3}{q}+{r}\:=\:\mathrm{3}}\end{cases}\:{or}\:\begin{cases}{{p}+{q}+\mathrm{2}{r}\:=\:\mathrm{1}}\\{\:\:\:\:\:\:{q}−\mathrm{3}{r}\:=\:−\mathrm{3}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}{r}\:=\:\mathrm{10}}\end{cases} \\ $$$${This}\:{unique}\:{solution}\:{of}\:{the}\:{triangular} \\ $$$${system}\:{is}\:\begin{cases}{{p}\:=\:−\mathrm{6}}\\{{q}\:=\:\mathrm{3}}\\{{r}\:=\:\mathrm{2}}\end{cases}.\:{Thus}\:{v}\:=\:−\mathrm{6}{u}_{\mathrm{1}} +\mathrm{3}{u}_{\mathrm{2}} +\mathrm{2}{u}_{\mathrm{3}} \\ $$$$ \\ $$
