
Question Number 118081 by bemath last updated on 15/Oct/20
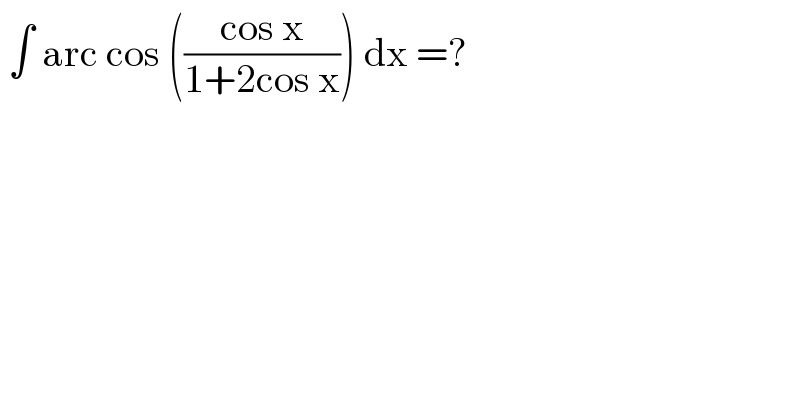
$$\:\int\:\mathrm{arc}\:\mathrm{cos}\:\left(\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{2cos}\:\mathrm{x}}\right)\:\mathrm{dx}\:=? \\ $$
Commented by MJS_new last updated on 15/Oct/20
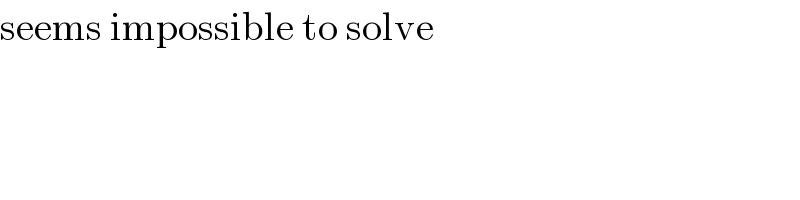
$$\mathrm{seems}\:\mathrm{impossible}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by MJS_new last updated on 16/Oct/20

$$\mathrm{this}\:\mathrm{is}\:\mathrm{one}\:\mathrm{version}\:\mathrm{of}\:\mathrm{the}\:\mathrm{Coxeter}\:\mathrm{Integral} \\ $$$$\mathrm{but}\:\mathrm{it}\:\mathrm{needs}\:\mathrm{borders} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{arccos}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{2cos}\:{x}}\:{dx}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$$$\mathrm{see}\:\mathrm{the}\:\mathrm{video}\:\mathrm{or}\:\mathrm{search}\:\mathrm{the}\:\mathrm{web} \\ $$
Commented by bemath last updated on 16/Oct/20

$${thank}\:{sir} \\ $$
Answered by AbduraufKodiriy last updated on 15/Oct/20
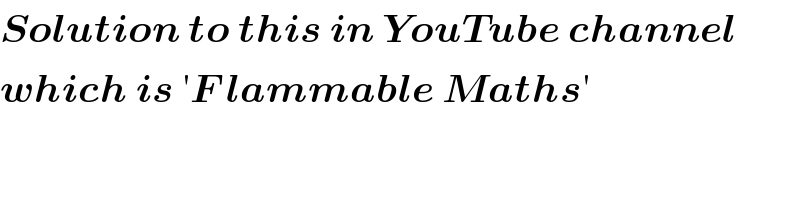
$$\boldsymbol{{Solution}}\:\boldsymbol{{to}}\:\boldsymbol{{this}}\:\boldsymbol{{in}}\:\boldsymbol{{YouTube}}\:\boldsymbol{{channel}} \\ $$$$\boldsymbol{{which}}\:\boldsymbol{{is}}\:'\boldsymbol{{F}}\:\boldsymbol{{lammable}}\:\boldsymbol{{Maths}}' \\ $$
