
Question Number 117979 by mnjuly1970 last updated on 14/Oct/20
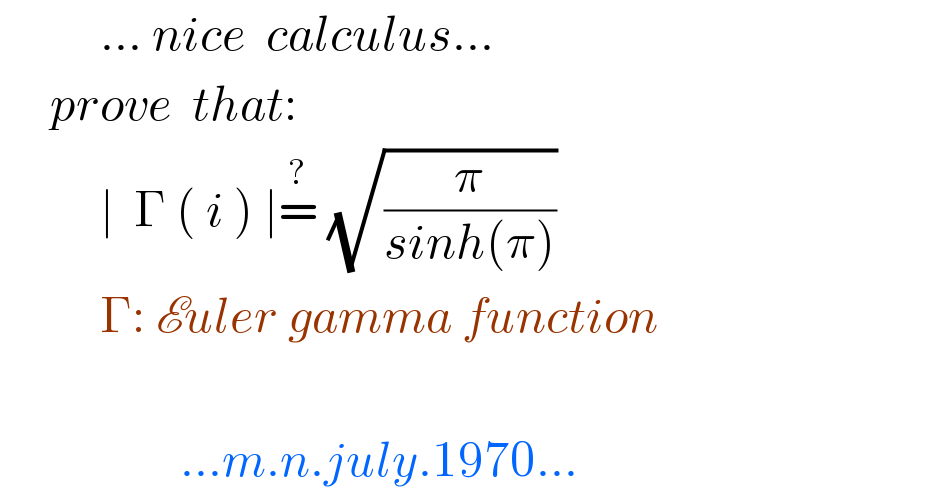
$$\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:{calculus}... \\ $$$$\:\:\:\:\:{prove}\:\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mid\:\:\Gamma\:\left(\:{i}\:\right)\:\mid\overset{?} {=}\:\sqrt{\frac{\pi}{{sinh}\left(\pi\right)}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Gamma:\:\mathscr{E}{uler}\:{gamma}\:{function}\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$
Commented by Lordose last updated on 14/Oct/20
THEY ARE NOT EQUAL
Answered by mindispower last updated on 14/Oct/20
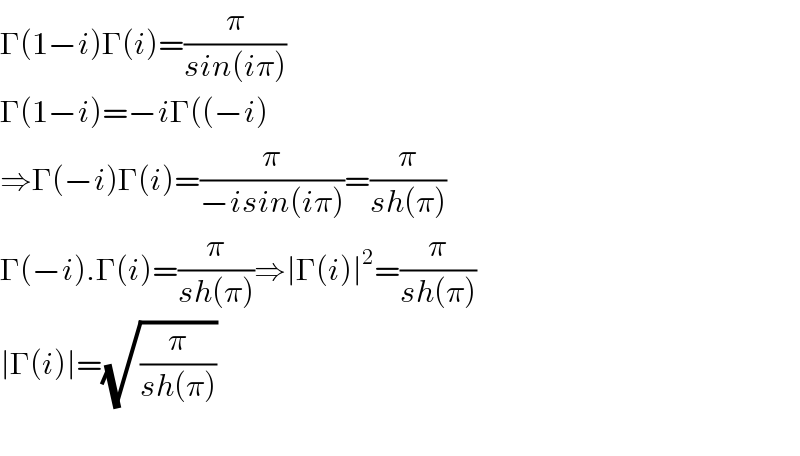
$$\Gamma\left(\mathrm{1}−{i}\right)\Gamma\left({i}\right)=\frac{\pi}{{sin}\left({i}\pi\right)} \\ $$$$\Gamma\left(\mathrm{1}−{i}\right)=−{i}\Gamma\left(\left(−{i}\right)\right. \\ $$$$\Rightarrow\Gamma\left(−{i}\right)\Gamma\left({i}\right)=\frac{\pi}{−{isin}\left({i}\pi\right)}=\frac{\pi}{{sh}\left(\pi\right)} \\ $$$$\Gamma\left(−{i}\right).\Gamma\left({i}\right)=\frac{\pi}{{sh}\left(\pi\right)}\Rightarrow\mid\Gamma\left({i}\right)\mid^{\mathrm{2}} =\frac{\pi}{{sh}\left(\pi\right)} \\ $$$$\mid\Gamma\left({i}\right)\mid=\sqrt{\frac{\pi}{{sh}\left(\pi\right)}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Oct/20

$${thank}\:{you} \\ $$
Commented by mindispower last updated on 14/Oct/20

$${withe}\:{pleasur} \\ $$
