
Question Number 117926 by bemath last updated on 14/Oct/20
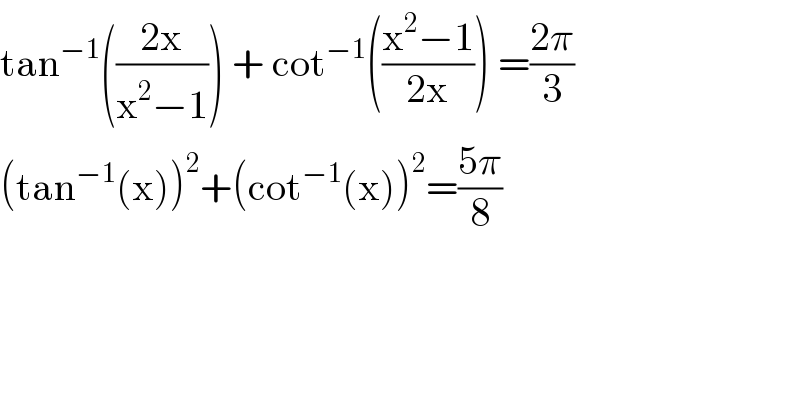
$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\:+\:\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2x}}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} +\left(\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} =\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 14/Oct/20
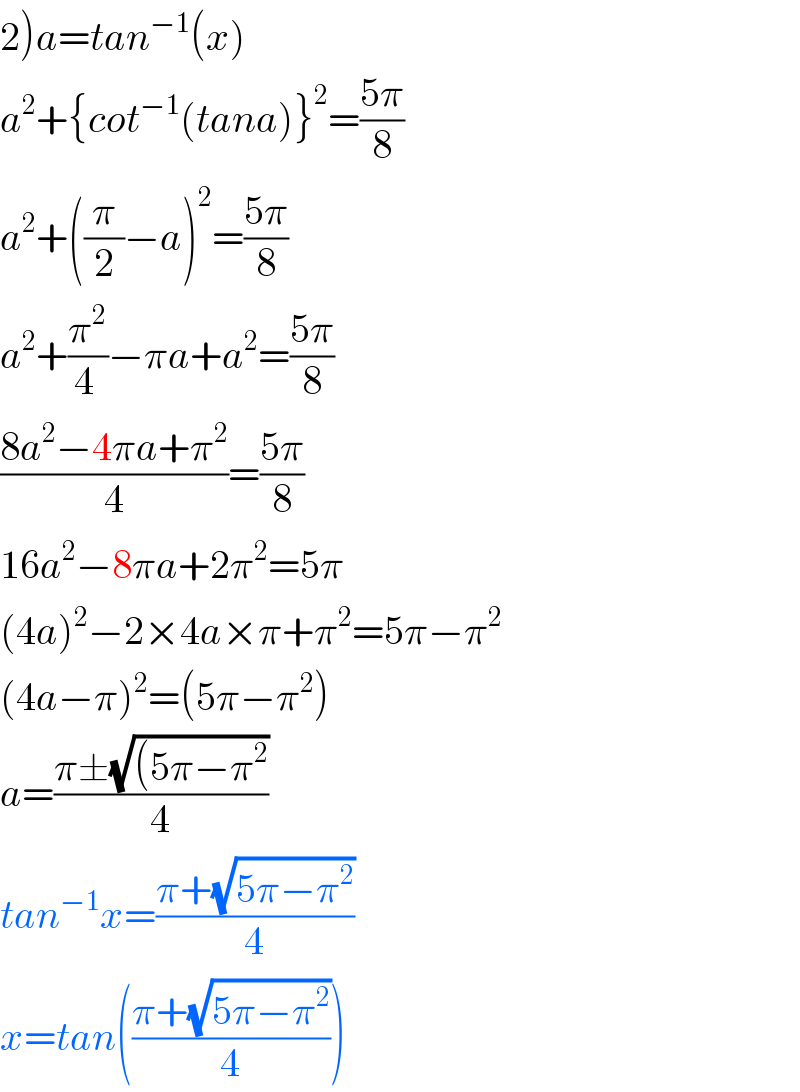
$$\left.\mathrm{2}\right){a}={tan}^{−\mathrm{1}} \left({x}\right) \\ $$$${a}^{\mathrm{2}} +\left\{{cot}^{−\mathrm{1}} \left({tana}\right)\right\}^{\mathrm{2}} =\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$${a}^{\mathrm{2}} +\left(\frac{\pi}{\mathrm{2}}−{a}\right)^{\mathrm{2}} =\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$${a}^{\mathrm{2}} +\frac{\pi^{\mathrm{2}} }{\mathrm{4}\:}−\pi{a}+{a}^{\mathrm{2}} =\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$$\frac{\mathrm{8}{a}^{\mathrm{2}} −\mathrm{4}\pi{a}+\pi^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$$\mathrm{16}{a}^{\mathrm{2}} −\mathrm{8}\pi{a}+\mathrm{2}\pi^{\mathrm{2}} =\mathrm{5}\pi \\ $$$$\left(\mathrm{4}{a}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{4}{a}×\pi+\pi^{\mathrm{2}} =\mathrm{5}\pi−\pi^{\mathrm{2}} \\ $$$$\left(\mathrm{4}{a}−\pi\right)^{\mathrm{2}} =\left(\mathrm{5}\pi−\pi^{\mathrm{2}} \right) \\ $$$${a}=\frac{\pi\pm\sqrt{\left(\mathrm{5}\pi−\pi^{\mathrm{2}} \right.}}{\mathrm{4}} \\ $$$${tan}^{−\mathrm{1}} {x}=\frac{\pi+\sqrt{\mathrm{5}\pi−\pi^{\mathrm{2}} }}{\mathrm{4}} \\ $$$${x}={tan}\left(\frac{\pi+\sqrt{\mathrm{5}\pi−\pi^{\mathrm{2}} }}{\mathrm{4}}\right) \\ $$
Answered by TANMAY PANACEA last updated on 14/Oct/20
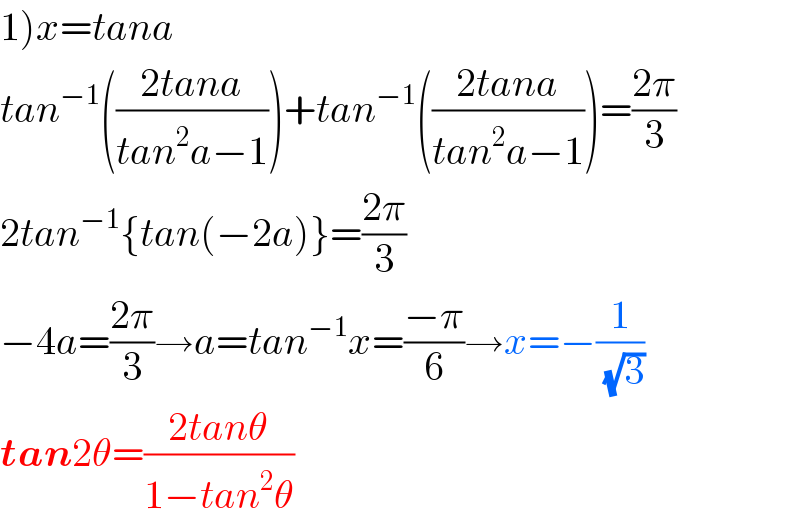
$$\left.\mathrm{1}\right){x}={tana} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{tana}}{{tan}^{\mathrm{2}} {a}−\mathrm{1}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{tana}}{{tan}^{\mathrm{2}} {a}−\mathrm{1}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{2}{tan}^{−\mathrm{1}} \left\{{tan}\left(−\mathrm{2}{a}\right)\right\}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$−\mathrm{4}{a}=\frac{\mathrm{2}\pi}{\mathrm{3}}\rightarrow{a}={tan}^{−\mathrm{1}} {x}=\frac{−\pi}{\mathrm{6}}\rightarrow{x}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\boldsymbol{{tan}}\mathrm{2}\theta=\frac{\mathrm{2}{tan}\theta}{\mathrm{1}−{tan}^{\mathrm{2}} \theta} \\ $$
Commented by bemath last updated on 14/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by bobhans last updated on 14/Oct/20

$$\left(\mathrm{1}\right)\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{for}\:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:>\:\mathrm{0}\:\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2x}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{2tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:;\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\sqrt{\mathrm{3}}\:;\:\sqrt{\mathrm{3}}\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\:=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{12}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{2}\pm\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{x}\:=\:\sqrt{\mathrm{3}}\:\mathrm{or}\:\mathrm{x}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{for}\:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:<\:\mathrm{0}\:\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2x}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)+\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\:=\:−\frac{\pi}{\mathrm{3}};\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)=−\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:;\:\mathrm{x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}\:=\:\frac{−\mathrm{2}\sqrt{\mathrm{3}}\:\pm\:\sqrt{\mathrm{12}+\mathrm{4}}}{\mathrm{2}}\:=\:\frac{−\mathrm{2}\sqrt{\mathrm{3}}\pm\mathrm{4}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}\:=\:−\sqrt{\mathrm{3}}\:+\mathrm{2}\:\mathrm{or}\:\mathrm{x}\:=\:−\sqrt{\mathrm{3}}−\mathrm{2}\: \\ $$
Commented by bemath last updated on 14/Oct/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
