
Question Number 117826 by snipers237 last updated on 13/Oct/20
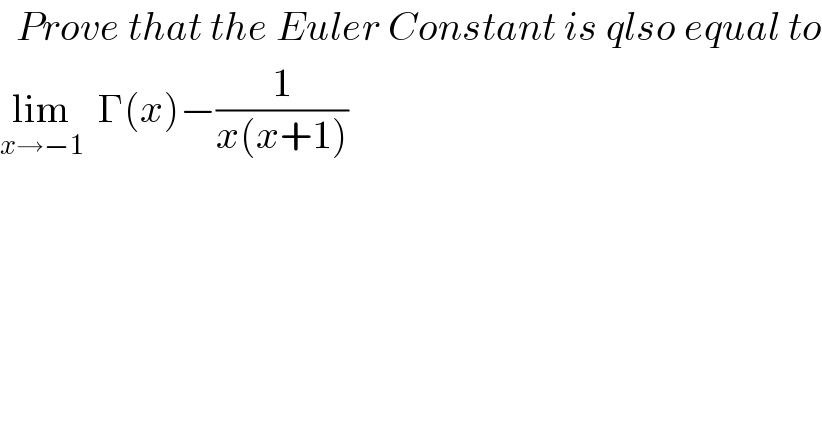
$$\:\:{Prove}\:{that}\:{the}\:{Euler}\:{Constant}\:{is}\:{qlso}\:{equal}\:{to} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\:\Gamma\left({x}\right)−\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)} \\ $$
Answered by mnjuly1970 last updated on 14/Oct/20
![solution:: lim_(x→−1) [Γ(x)−(1/(x(x+1)))] =lim_(x→−1 ) (((Γ(x+2)−1)/(x(x+1)))) =^(l′hospital) lim_(x→−1 ) (((Γ ′(x+2))/(2x+1))) =((Γ′(1))/(−1))=−Γ′(1)=−ψ(1)Γ(1)=γ where:: γ is Euler− Masheroni constant ... m.n.1970...](Q117892.png)
$${solution}:: \\ $$$$\:{lim}_{{x}\rightarrow−\mathrm{1}} \:\left[\Gamma\left({x}\right)−\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}\right] \\ $$$$\:={lim}_{{x}\rightarrow−\mathrm{1}\:} \:\left(\frac{\Gamma\left({x}+\mathrm{2}\right)−\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}\right) \\ $$$$\:\overset{{l}'{hospital}} {=}{lim}_{{x}\rightarrow−\mathrm{1}\:} \left(\frac{\Gamma\:'\left({x}+\mathrm{2}\right)}{\mathrm{2}{x}+\mathrm{1}}\right) \\ $$$$\:\:\:\: \\ $$$$=\frac{\Gamma'\left(\mathrm{1}\right)}{−\mathrm{1}}=−\Gamma'\left(\mathrm{1}\right)=−\psi\left(\mathrm{1}\right)\Gamma\left(\mathrm{1}\right)=\gamma \\ $$$$\:{where}::\:\:\gamma\:\:{is}\:\mathscr{E}{uler}− \\ $$$$\mathscr{M}{asheroni}\:{constant} \\ $$$$\:\:\:\:\:\:\:\:\:...\:{m}.{n}.\mathrm{1970}... \\ $$
