
Question Number 117557 by abdullahquwatan last updated on 12/Oct/20

$$\mathrm{second}\:\mathrm{derivative} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} =\mathrm{5} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
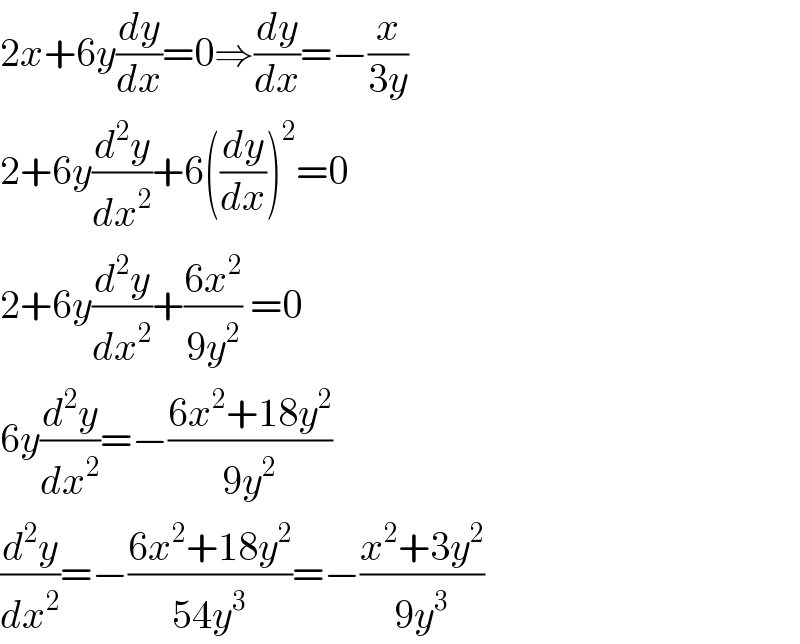
$$\mathrm{2}{x}+\mathrm{6}{y}\frac{{dy}}{{dx}}=\mathrm{0}\Rightarrow\frac{{dy}}{{dx}}=−\frac{{x}}{\mathrm{3}{y}} \\ $$$$\mathrm{2}+\mathrm{6}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{6}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}+\mathrm{6}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\mathrm{6}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{18}{y}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{2}} } \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{18}{y}^{\mathrm{2}} }{\mathrm{54}{y}^{\mathrm{3}} }=−\frac{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{3}} } \\ $$
Commented by abdullahquwatan last updated on 12/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by abdullahquwatan last updated on 12/Oct/20
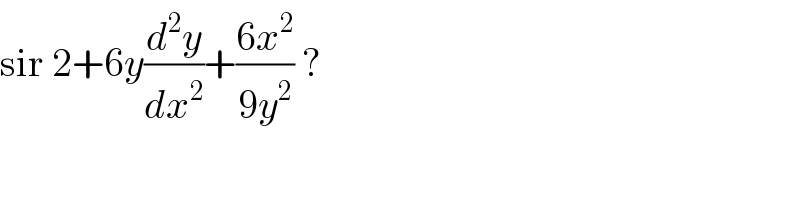
$$\mathrm{sir}\:\mathrm{2}+\mathrm{6}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{2}} }\:? \\ $$
Commented by abdullahquwatan last updated on 12/Oct/20
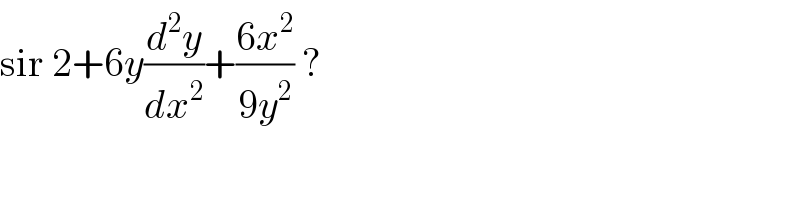
$$\mathrm{sir}\:\mathrm{2}+\mathrm{6}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{2}} }\:? \\ $$
Commented by Dwaipayan Shikari last updated on 12/Oct/20
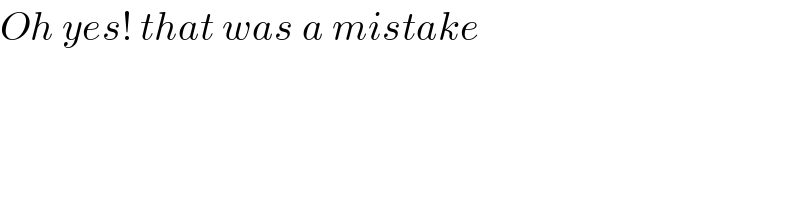
$${Oh}\:{yes}!\:{that}\:{was}\:{a}\:{mistake} \\ $$
Commented by abdullahquwatan last updated on 12/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
