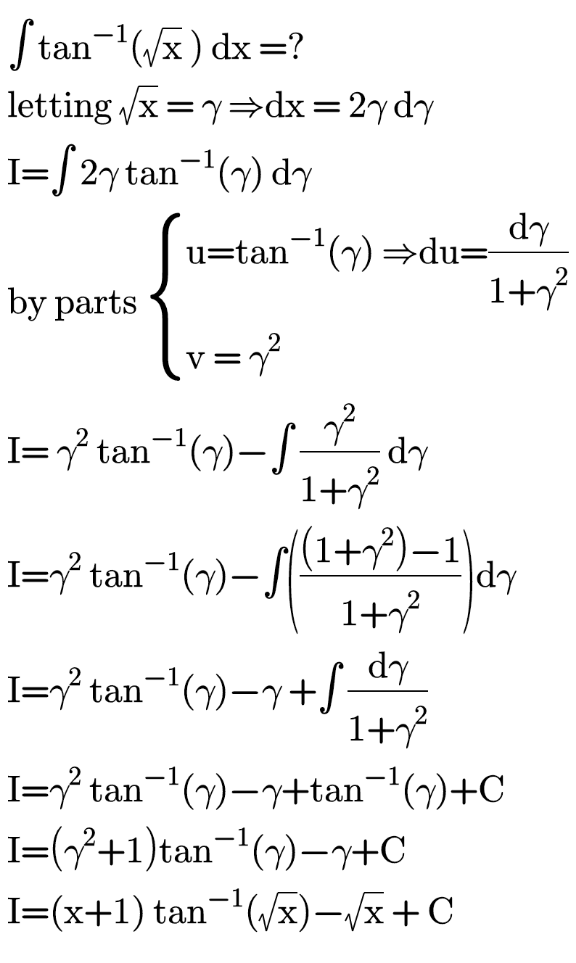Question Number 117342 by bemath last updated on 11/Oct/20
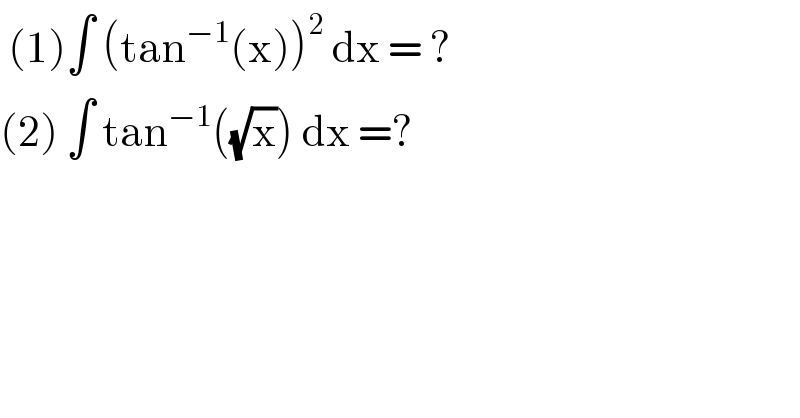
$$\:\left(\mathrm{1}\right)\int\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} \:\mathrm{dx}\:=\:? \\ $$$$\left(\mathrm{2}\right)\:\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\:=? \\ $$
Answered by mathmax by abdo last updated on 11/Oct/20
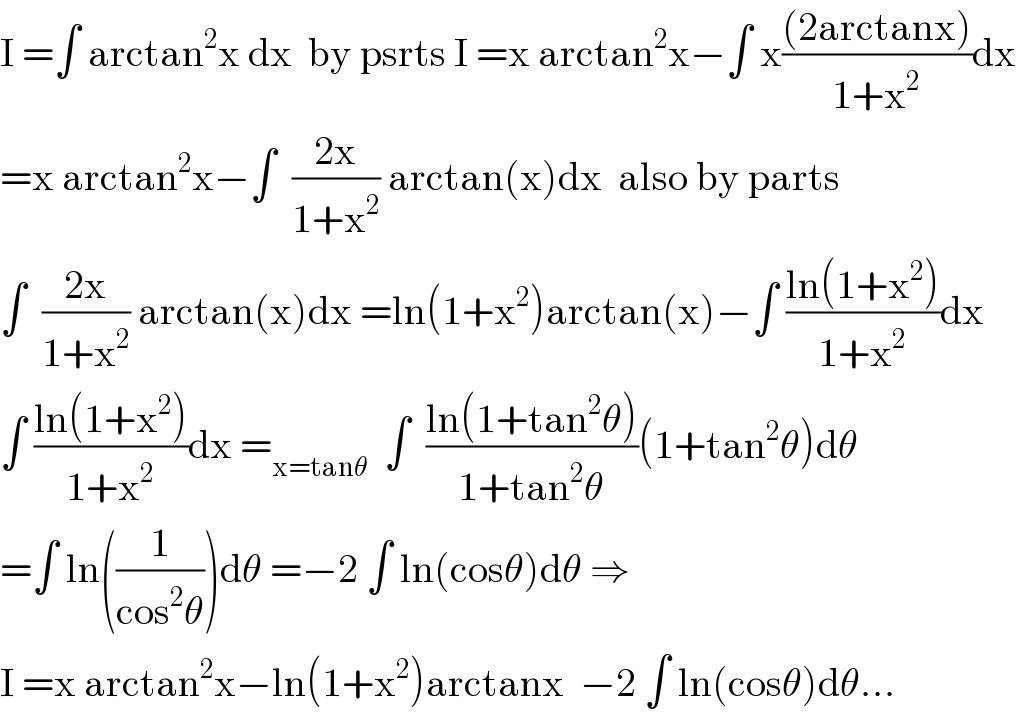
$$\mathrm{I}\:=\int\:\mathrm{arctan}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:\:\mathrm{by}\:\mathrm{psrts}\:\mathrm{I}\:=\mathrm{x}\:\mathrm{arctan}^{\mathrm{2}} \mathrm{x}−\int\:\mathrm{x}\frac{\left(\mathrm{2arctanx}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{x}\:\mathrm{arctan}^{\mathrm{2}} \mathrm{x}−\int\:\:\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{arctan}\left(\mathrm{x}\right)\mathrm{dx}\:\:\mathrm{also}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int\:\:\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{arctan}\left(\mathrm{x}\right)\mathrm{dx}\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{arctan}\left(\mathrm{x}\right)−\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\int\:\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\int\:\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\right)\mathrm{d}\theta\:=−\mathrm{2}\:\int\:\mathrm{ln}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{x}\:\mathrm{arctan}^{\mathrm{2}} \mathrm{x}−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{arctanx}\:\:−\mathrm{2}\:\int\:\mathrm{ln}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta... \\ $$
Commented by mathmax by abdo last updated on 11/Oct/20
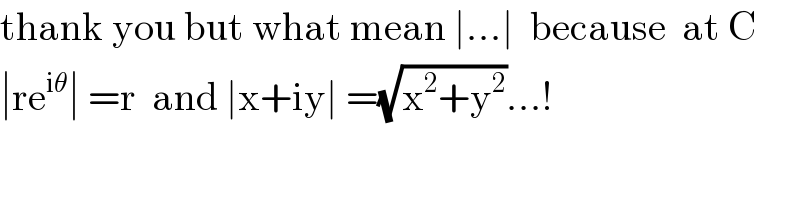
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{but}\:\mathrm{what}\:\mathrm{mean}\:\mid...\mid\:\:\mathrm{because}\:\:\mathrm{at}\:\mathrm{C} \\ $$$$\mid\mathrm{re}^{\mathrm{i}\theta} \mid\:=\mathrm{r}\:\:\mathrm{and}\:\mid\mathrm{x}+\mathrm{iy}\mid\:=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }...! \\ $$
Commented by bemath last updated on 11/Oct/20

$$\mathrm{the}\:\mathrm{last}\:\mathrm{term}\: \\ $$$$\int\:\mathrm{ln}\:\left(\mathrm{cos}\:\theta\right)\:\mathrm{d}\theta\:=? \\ $$
Commented by Lordose last updated on 11/Oct/20
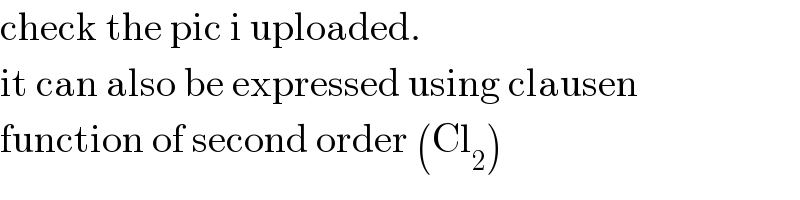
$$\mathrm{check}\:\mathrm{the}\:\mathrm{pic}\:\mathrm{i}\:\mathrm{uploaded}. \\ $$$$\mathrm{it}\:\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{expressed}\:\mathrm{using}\:\mathrm{clausen} \\ $$$$\mathrm{function}\:\mathrm{of}\:\mathrm{second}\:\mathrm{order}\:\left(\mathrm{Cl}_{\mathrm{2}} \right) \\ $$
Answered by bemath last updated on 11/Oct/20