
Question Number 117095 by bemath last updated on 09/Oct/20
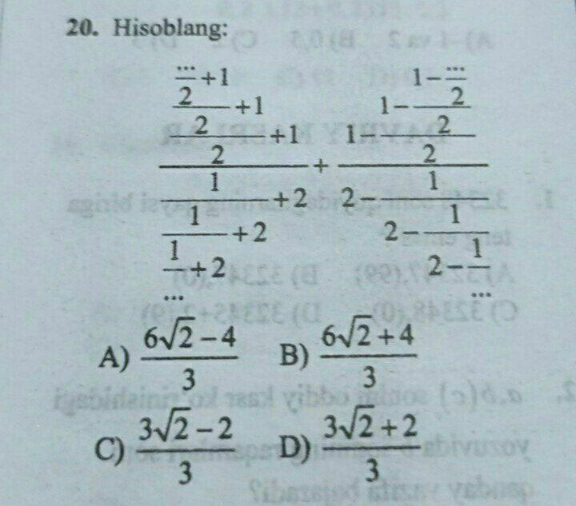
Answered by Olaf last updated on 09/Oct/20
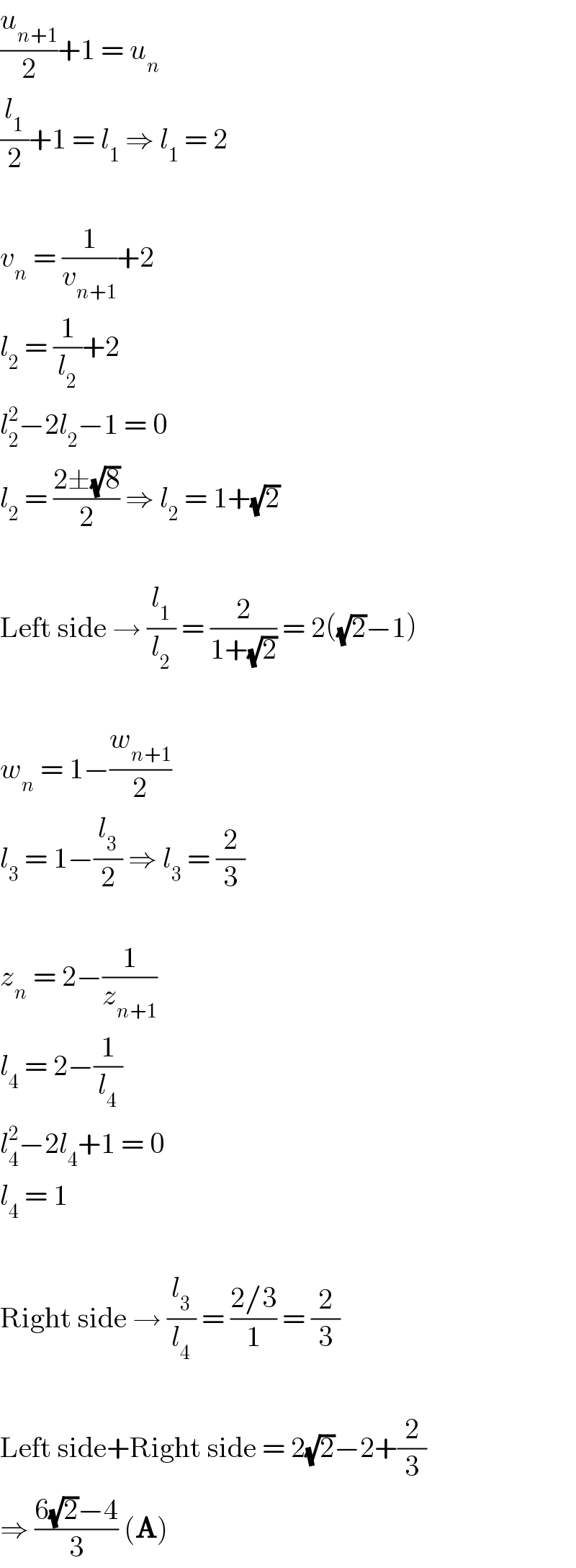
$$\frac{{u}_{{n}+\mathrm{1}} }{\mathrm{2}}+\mathrm{1}\:=\:{u}_{{n}} \\ $$$$\frac{{l}_{\mathrm{1}} }{\mathrm{2}}+\mathrm{1}\:=\:{l}_{\mathrm{1}} \:\Rightarrow\:{l}_{\mathrm{1}} \:=\:\mathrm{2} \\ $$$$ \\ $$$${v}_{{n}} \:=\:\frac{\mathrm{1}}{{v}_{{n}+\mathrm{1}} }+\mathrm{2} \\ $$$${l}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{{l}_{\mathrm{2}} }+\mathrm{2} \\ $$$${l}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{l}_{\mathrm{2}} −\mathrm{1}\:=\:\mathrm{0} \\ $$$${l}_{\mathrm{2}} \:=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{8}}}{\mathrm{2}}\:\Rightarrow\:{l}_{\mathrm{2}} \:=\:\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Left}\:\mathrm{side}\:\rightarrow\:\frac{{l}_{\mathrm{1}} }{{l}_{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\:=\:\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$ \\ $$$${w}_{{n}} \:=\:\mathrm{1}−\frac{{w}_{{n}+\mathrm{1}} }{\mathrm{2}} \\ $$$${l}_{\mathrm{3}} \:=\:\mathrm{1}−\frac{{l}_{\mathrm{3}} }{\mathrm{2}}\:\Rightarrow\:{l}_{\mathrm{3}} \:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$${z}_{{n}} \:=\:\mathrm{2}−\frac{\mathrm{1}}{{z}_{{n}+\mathrm{1}} } \\ $$$${l}_{\mathrm{4}} \:=\:\mathrm{2}−\frac{\mathrm{1}}{{l}_{\mathrm{4}} } \\ $$$${l}_{\mathrm{4}} ^{\mathrm{2}} −\mathrm{2}{l}_{\mathrm{4}} +\mathrm{1}\:=\:\mathrm{0} \\ $$$${l}_{\mathrm{4}} \:=\:\mathrm{1} \\ $$$$ \\ $$$$\mathrm{Right}\:\mathrm{side}\:\rightarrow\:\frac{{l}_{\mathrm{3}} }{{l}_{\mathrm{4}} }\:=\:\frac{\mathrm{2}/\mathrm{3}}{\mathrm{1}}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{Left}\:\mathrm{side}+\mathrm{Right}\:\mathrm{side}\:=\:\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:\frac{\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{4}}{\mathrm{3}}\:\left(\boldsymbol{\mathrm{A}}\right) \\ $$
