
Question Number 117026 by bemath last updated on 08/Oct/20
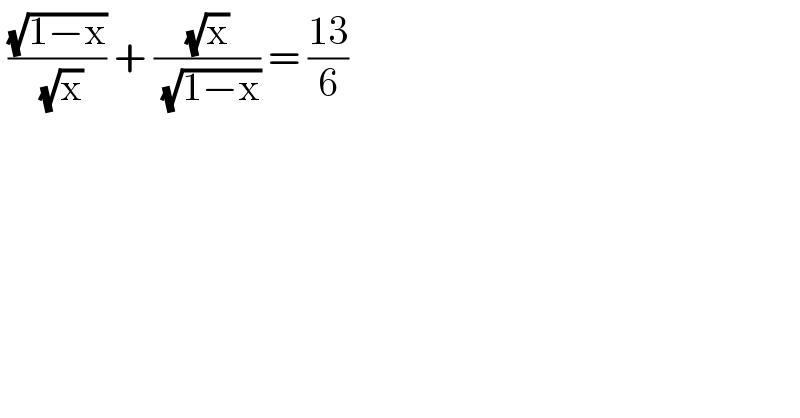
$$\:\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{x}}}\:+\:\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\:=\:\frac{\mathrm{13}}{\mathrm{6}} \\ $$
Answered by 1549442205PVT last updated on 09/Oct/20

$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{for}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{is}\:\mathrm{defined}\:\mathrm{as}\:\mathrm{0}<\mathrm{x}<\mathrm{1}\left(\ast\right) \\ $$$$\:\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{x}}}\:+\:\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\:=\:\frac{\mathrm{13}}{\mathrm{6}}\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{1}−\mathrm{x}+\mathrm{x}}{\:\sqrt{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\Leftrightarrow\mathrm{6}=\mathrm{13}\sqrt{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)}\Leftrightarrow\mathrm{36}=\mathrm{169}\left(\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{169x}^{\mathrm{2}} −\mathrm{169x}+\mathrm{36}=\mathrm{0} \\ $$$$\Delta=\mathrm{169}^{\mathrm{2}} −\mathrm{4}.\mathrm{169}.\mathrm{36}=\mathrm{169}.\mathrm{25}=\mathrm{65}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{169}\pm\mathrm{65}}{\mathrm{2}.\mathrm{169}}=\frac{\mathrm{13}\pm\mathrm{5}}{\mathrm{2}.\mathrm{13}}\in\left\{\frac{\mathrm{4}}{\mathrm{13}},\frac{\mathrm{9}}{\mathrm{13}}\right\} \\ $$$$\mathrm{both}\:\mathrm{satisfy}\:\left(\ast\right) \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{two}\:\mathrm{roots} \\ $$$$\mathrm{x}\in\left\{\frac{\mathrm{4}}{\mathrm{13}},\frac{\mathrm{9}}{\mathrm{13}}\right\} \\ $$
Commented by bemath last updated on 09/Oct/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Answered by TANMAY PANACEA last updated on 09/Oct/20
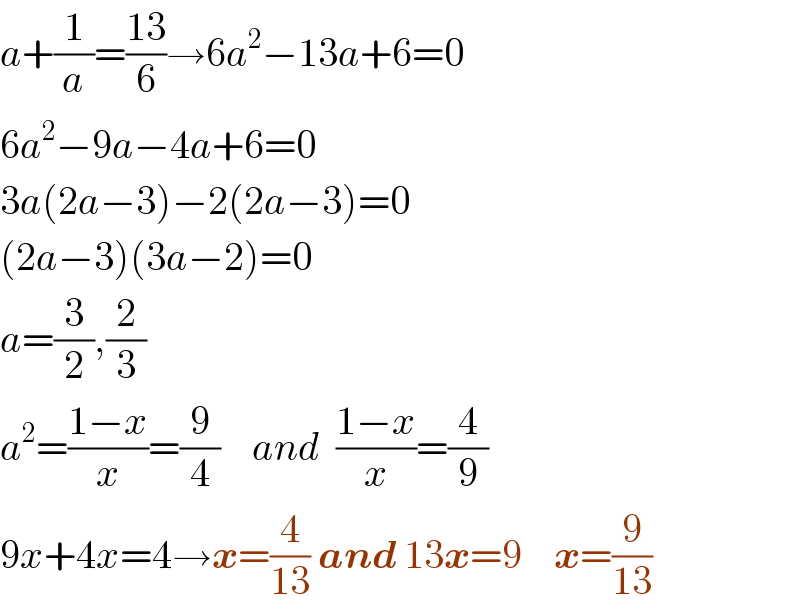
$${a}+\frac{\mathrm{1}}{{a}}=\frac{\mathrm{13}}{\mathrm{6}}\rightarrow\mathrm{6}{a}^{\mathrm{2}} −\mathrm{13}{a}+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{6}{a}^{\mathrm{2}} −\mathrm{9}{a}−\mathrm{4}{a}+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{3}{a}\left(\mathrm{2}{a}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{a}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{a}−\mathrm{3}\right)\left(\mathrm{3}{a}−\mathrm{2}\right)=\mathrm{0} \\ $$$${a}=\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{1}−{x}}{{x}}=\frac{\mathrm{9}}{\mathrm{4}}\:\:\:\:{and}\:\:\frac{\mathrm{1}−{x}}{{x}}=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\mathrm{9}{x}+\mathrm{4}{x}=\mathrm{4}\rightarrow\boldsymbol{{x}}=\frac{\mathrm{4}}{\mathrm{13}}\:\boldsymbol{{and}}\:\mathrm{13}\boldsymbol{{x}}=\mathrm{9}\:\:\:\:\boldsymbol{{x}}=\frac{\mathrm{9}}{\mathrm{13}} \\ $$
