
Question Number 116996 by mnjuly1970 last updated on 08/Oct/20

Answered by mindispower last updated on 09/Oct/20
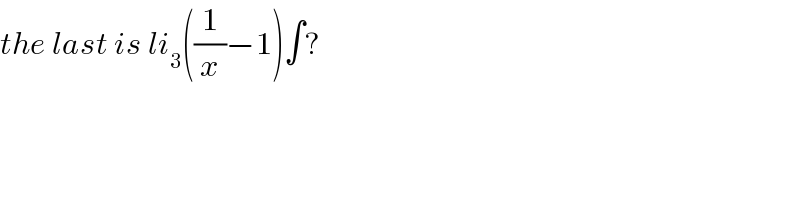
$${the}\:{last}\:{is}\:{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)\int? \\ $$
Commented by mnjuly1970 last updated on 09/Oct/20

$${no}\: \\ $$$${li}_{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$
Commented by mnjuly1970 last updated on 09/Oct/20
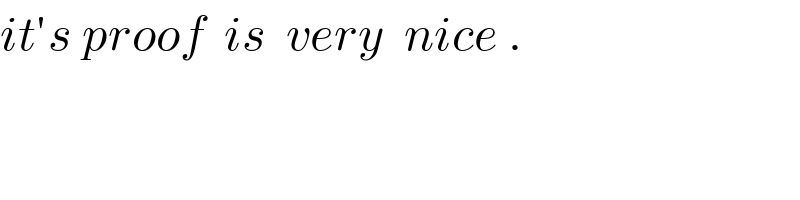
$${it}'{s}\:{proof}\:\:{is}\:\:{very}\:\:{nice}\:. \\ $$
Answered by mindispower last updated on 19/Oct/20
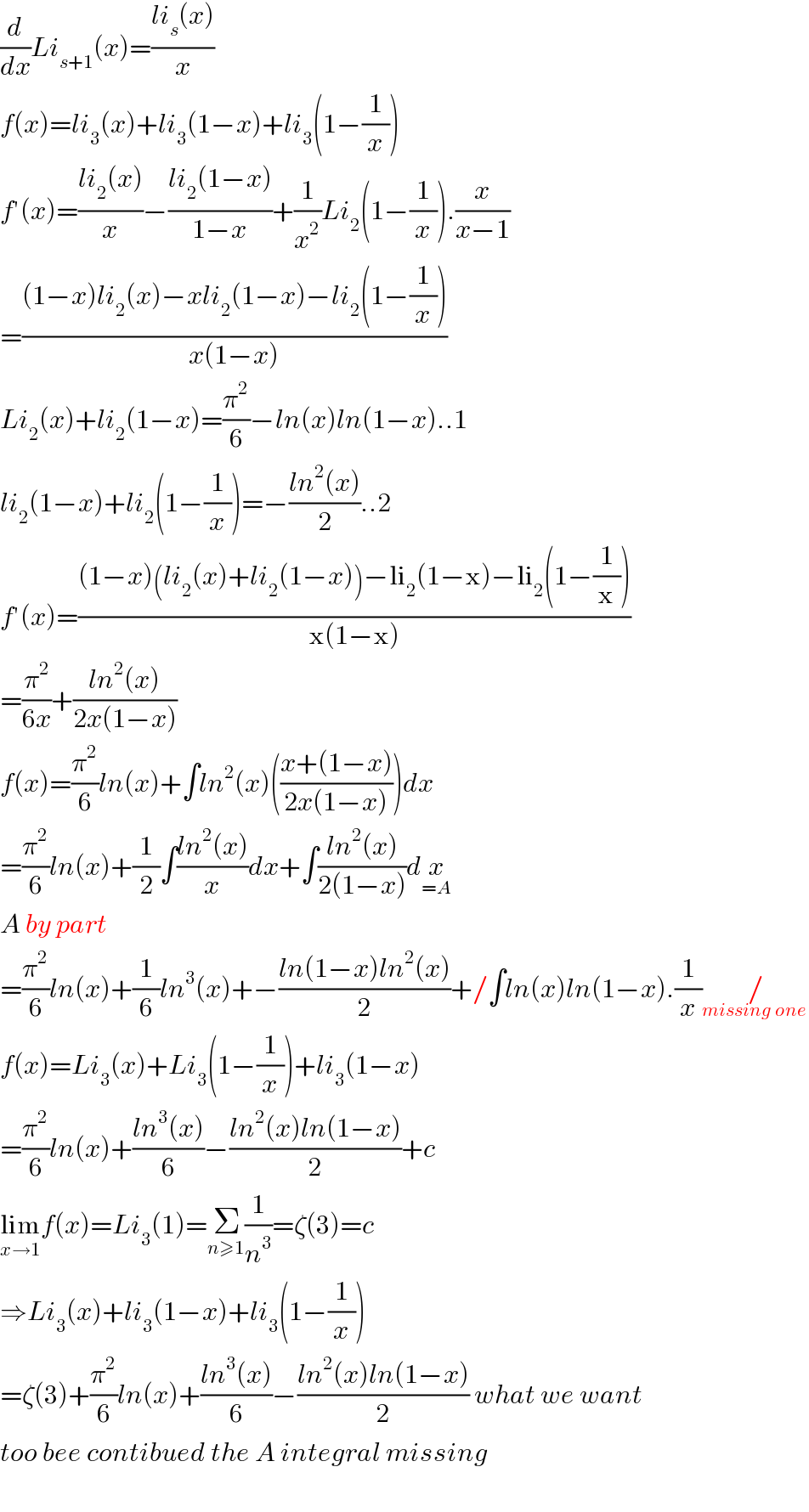
$$\frac{{d}}{{dx}}{Li}_{{s}+\mathrm{1}} \left({x}\right)=\frac{{li}_{{s}} \left({x}\right)}{{x}} \\ $$$${f}\left({x}\right)={li}_{\mathrm{3}} \left({x}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−{x}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${f}'\left({x}\right)=\frac{{li}_{\mathrm{2}} \left({x}\right)}{{x}}−\frac{{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{Li}_{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right).\frac{{x}}{{x}−\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{1}−{x}\right){li}_{\mathrm{2}} \left({x}\right)−{xli}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)−{li}_{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)}{{x}\left(\mathrm{1}−{x}\right)} \\ $$$${Li}_{\mathrm{2}} \left({x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right)..\mathrm{1} \\ $$$${li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)=−\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}..\mathrm{2} \\ $$$${f}'\left({x}\right)=\frac{\left(\mathrm{1}−{x}\right)\left({li}_{\mathrm{2}} \left({x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)\right)−\mathrm{li}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)−\mathrm{li}_{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}{x}}+\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}{x}\left(\mathrm{1}−{x}\right)} \\ $$$${f}\left({x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left({x}\right)+\int{ln}^{\mathrm{2}} \left({x}\right)\left(\frac{{x}+\left(\mathrm{1}−{x}\right)}{\mathrm{2}{x}\left(\mathrm{1}−{x}\right)}\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{ln}^{\mathrm{2}} \left({x}\right)}{{x}}{dx}+\int\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}\left(\mathrm{1}−{x}\right)}{d}\underset{={A}} {{x}} \\ $$$${A}\:{by}\:{part} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{6}}{ln}^{\mathrm{3}} \left({x}\right)+−\frac{{ln}\left(\mathrm{1}−{x}\right){ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}+/\int{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right).\frac{\mathrm{1}}{{x}}\underset{{missing}\:{one}\:} {/} \\ $$$${f}\left({x}\right)={Li}_{\mathrm{3}} \left({x}\right)+{Li}_{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−{x}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left({x}\right)+\frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{6}}−\frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}−{x}\right)}{\mathrm{2}}+{c} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{f}\left({x}\right)={Li}_{\mathrm{3}} \left(\mathrm{1}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }=\zeta\left(\mathrm{3}\right)={c} \\ $$$$\Rightarrow{Li}_{\mathrm{3}} \left({x}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−{x}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left({x}\right)+\frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{6}}−\frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}−{x}\right)}{\mathrm{2}}\:{what}\:{we}\:{want}\: \\ $$$${too}\:{bee}\:{contibued}\:{the}\:{A}\:{integral}\:{missing} \\ $$$$ \\ $$
