
Question Number 116844 by bemath last updated on 07/Oct/20
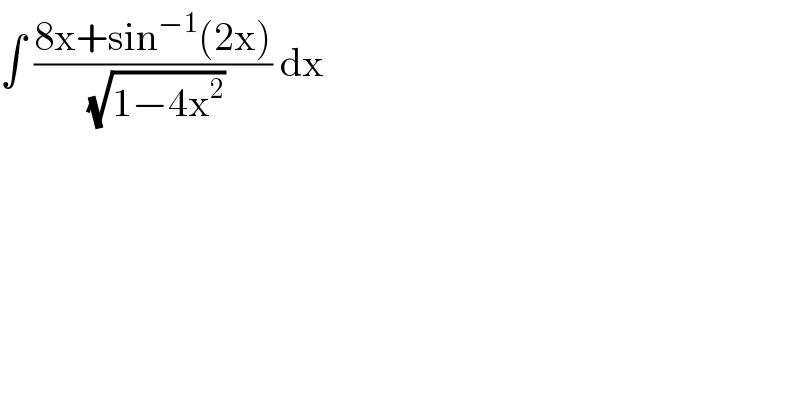
$$\int\:\frac{\mathrm{8x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 07/Oct/20
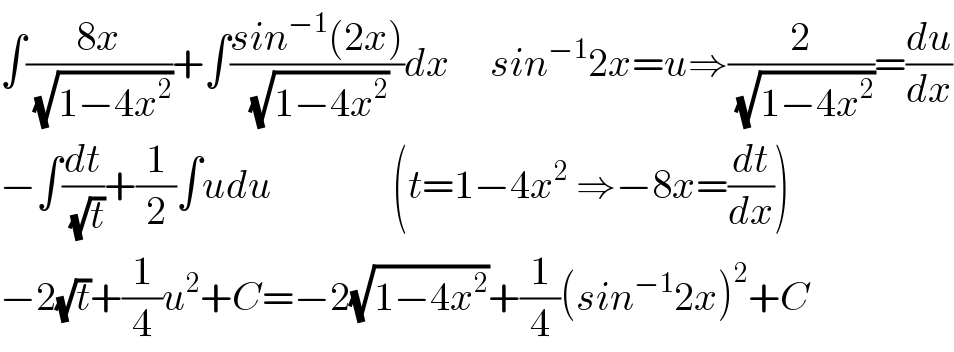
$$\int\frac{\mathrm{8}{x}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}+\int\frac{{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}{dx}\:\:\:\:\:{sin}^{−\mathrm{1}} \mathrm{2}{x}={u}\Rightarrow\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}=\frac{{du}}{{dx}} \\ $$$$−\int\frac{{dt}}{\:\sqrt{{t}}}+\frac{\mathrm{1}}{\mathrm{2}}\int{udu}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({t}=\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} \:\Rightarrow−\mathrm{8}{x}=\frac{{dt}}{{dx}}\right) \\ $$$$−\mathrm{2}\sqrt{{t}}+\frac{\mathrm{1}}{\mathrm{4}}{u}^{\mathrm{2}} +{C}=−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\left({sin}^{−\mathrm{1}} \mathrm{2}{x}\right)^{\mathrm{2}} +{C} \\ $$
