
Question Number 116796 by mnjuly1970 last updated on 08/Oct/20
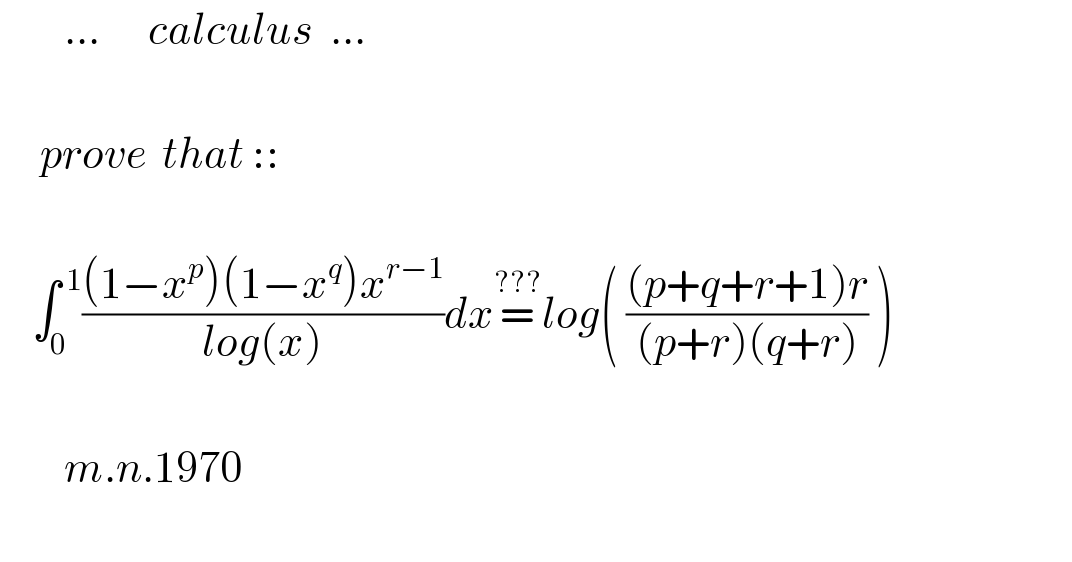
$$\:\:\:\:\:\:\:\:...\:\:\:\:\:\:{calculus}\:\:... \\ $$$$ \\ $$$$\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$ \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right){x}^{{r}−\mathrm{1}} }{{log}\left({x}\right)}{dx}\overset{???} {=}{log}\left(\:\frac{\left({p}+{q}+{r}+\mathrm{1}\right){r}}{\left({p}+{r}\right)\left({q}+{r}\right)}\:\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$$$\: \\ $$
Answered by mindispower last updated on 08/Oct/20

$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right){x}^{{r}−\mathrm{1}+{a}} }{{log}\left({x}\right)}{dx} \\ $$$${f}'\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right){x}^{{r}−\mathrm{1}+{a}} }{{log}\left({x}\right)}.{log}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{{r}+{a}−\mathrm{1}} +{x}^{{p}+{q}+{r}−\mathrm{1}+{a}} −{x}^{{p}+{r}−\mathrm{1}+{a}} −{x}^{{q}+{r}−\mathrm{1}+{a}} \right){dx}\:\: \\ $$$$=\frac{\mathrm{1}}{{r}+{a}}+\frac{\mathrm{1}}{{r}+{q}+{a}+\mathrm{1}}−\frac{\mathrm{1}}{{p}+{r}+{a}}−\frac{\mathrm{1}}{{q}+{r}+{a}} \\ $$$${we}\:{want}\:{f}\left(\mathrm{0}\right) \\ $$$${f}\left({a}\right)=\int\left(\frac{\mathrm{1}}{{r}+{a}}+\frac{\mathrm{1}}{{r}+{q}+{a}+\mathrm{1}+{p}}−\frac{\mathrm{1}}{{p}+{r}+{a}}−\frac{\mathrm{1}}{{q}+{r}+{a}}\right){da} \\ $$$$={ln}\frac{\left({r}+{a}\right)\left({r}+{q}+{p}+{a}+\mathrm{1}\right)}{\left({p}+{r}+{a}\right)\left({q}+{r}+{a}\right)}+{c} \\ $$$$\underset{{a}\rightarrow\infty} {\mathrm{lim}}{f}\left({a}\right)=\mathrm{0}\Rightarrow{c}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)={ln}\left(\frac{{r}\left({p}+{q}+{r}+\mathrm{1}\right)}{\left({p}+{r}\right)\left({q}+{r}\right)}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right){x}^{{r}−\mathrm{1}} }{{log}\left({x}\right)}{dx}={ln}\left(\frac{{r}\left({p}+{q}+{r}+\mathrm{1}\right)}{\left({p}+{r}\right)\left({q}+{r}\right)}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 08/Oct/20
$${tayyeballah}\:\:{bravo}\:\:{thank}\:{you}.. \\ $$
Commented by mindispower last updated on 08/Oct/20

$${withe}\:{Pleasur}\: \\ $$
