
Question Number 116779 by mathdave last updated on 06/Oct/20

$${solve} \\ $$$${x}^{{x}} =\mathrm{2} \\ $$
Answered by Dwaipayan Shikari last updated on 06/Oct/20
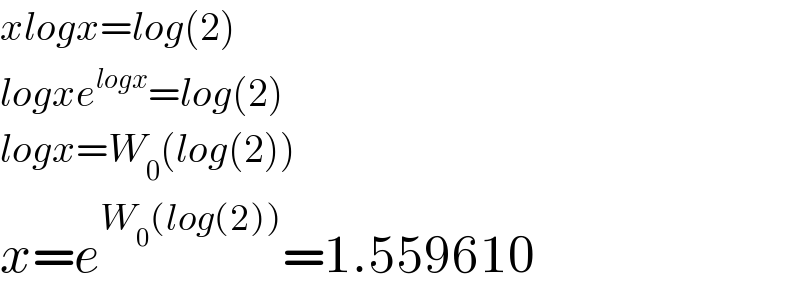
$${xlogx}={log}\left(\mathrm{2}\right) \\ $$$${logxe}^{{logx}} ={log}\left(\mathrm{2}\right) \\ $$$${logx}={W}_{\mathrm{0}} \left({log}\left(\mathrm{2}\right)\right) \\ $$$${x}={e}^{{W}_{\mathrm{0}} \left({log}\left(\mathrm{2}\right)\right)} =\mathrm{1}.\mathrm{559610} \\ $$
