
Question Number 116776 by abony1303 last updated on 06/Oct/20

$$\mathrm{Given}\:\mathrm{function}: \\ $$ $${f}\left({x}\right)=\begin{cases}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1},\:\:\mid{x}\mid<\mathrm{3}}\\{\mathrm{5x}−\mathrm{1},\:\:\mid{x}\mid\geqslant\mathrm{3}}\end{cases} \\ $$ $$\mathrm{Find}\:\mathrm{out}:\:{f}\left({x}^{\mathrm{2}} +\mathrm{7}\right)=? \\ $$ $$ \\ $$ $$\left.\mathrm{A}\left.\right)\left.\mathrm{5x}^{\mathrm{2}} −\mathrm{34}\:\:\:\:\:\mathrm{B}\right)\mathrm{2x}^{\mathrm{2}} +\mathrm{8}\:\:\:\mathrm{C}\right)\mathrm{5x}^{\mathrm{2}} +\mathrm{36} \\ $$ $$\left.\mathrm{D}\left.\right)\mathrm{5x}^{\mathrm{2}} +\mathrm{34}\:\:\:\:\mathrm{E}\right)\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7}\right)^{\mathrm{2}} +\mathrm{1} \\ $$ $$\mathrm{Please}\:\mathrm{help} \\ $$
Answered by floor(10²Eta[1]) last updated on 06/Oct/20
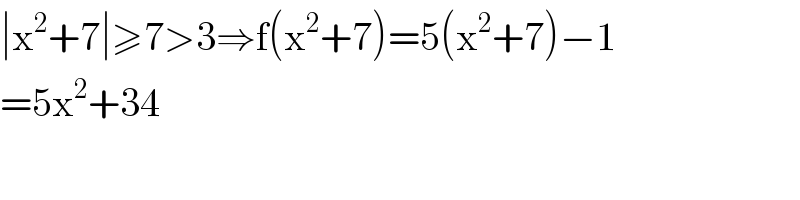
$$\mid\mathrm{x}^{\mathrm{2}} +\mathrm{7}\mid\geqslant\mathrm{7}>\mathrm{3}\Rightarrow\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7}\right)=\mathrm{5}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7}\right)−\mathrm{1} \\ $$ $$=\mathrm{5x}^{\mathrm{2}} +\mathrm{34} \\ $$
