
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 116746 by bemath last updated on 06/Oct/20
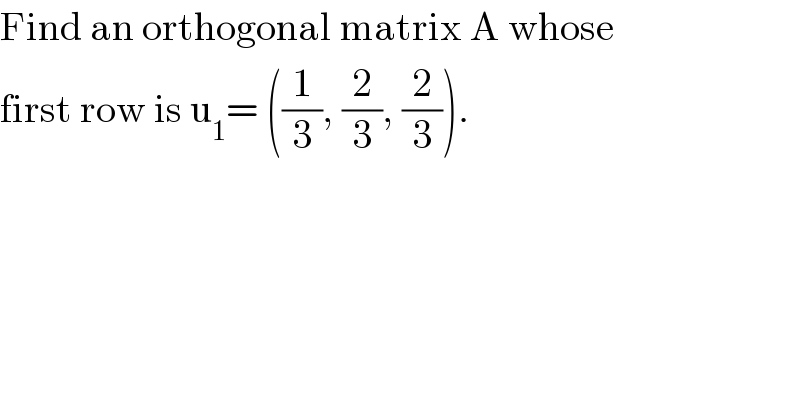
$$\mathrm{Find}\:\mathrm{an}\:\mathrm{orthogonal}\:\mathrm{matrix}\:\mathrm{A}\:\mathrm{whose} \\ $$$$\mathrm{first}\:\mathrm{row}\:\mathrm{is}\:\mathrm{u}_{\mathrm{1}} =\:\left(\frac{\mathrm{1}}{\mathrm{3}},\:\frac{\mathrm{2}}{\mathrm{3}},\:\frac{\mathrm{2}}{\mathrm{3}}\right). \\ $$
Answered by john santu last updated on 06/Oct/20

$${First}\:{step}\:{find}\:{a}\:{nonzero}\:{vector}\: \\ $$$${w}_{\mathrm{1}} =\left({x},{y},{z}\right)\:{that}\:{is}\:{orthogonal}\:{to}\:{u}_{\mathrm{1}} . \\ $$$${for}\:{which}\:\langle{u}_{\mathrm{1}} ,{w}_{\mathrm{1}} \rangle\:=\:\mathrm{0}=\frac{{x}}{\mathrm{3}}+\frac{\mathrm{2}{y}}{\mathrm{3}}+\frac{\mathrm{2}{z}}{\mathrm{3}} \\ $$$${or}\:{x}+\mathrm{2}{y}+\mathrm{2}{z}\:=\:\mathrm{0}\:.\:{One}\:{such}\:{solution} \\ $$$${is}\:{w}_{\mathrm{1}} =\left(\mathrm{0},\mathrm{1},−\mathrm{1}\right).\:{Normalize}\:{w}_{\mathrm{1}} \:{to}\: \\ $$$${obtain}\:{the}\:{second}\:{row}\:{of}\:{A},\:{u}_{\mathrm{2}} =\left(\mathrm{0},\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}},−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${Next}\:{step}\:{find}\:{a}\:{nonzero}\:{vector}\:{w}_{\mathrm{2}} =\left({x},{y},{z}\right) \\ $$$${that}\:{is}\:{orthogonal}\:{to}\:{both}\:{u}_{\mathrm{1}} \:{and}\:{u}_{\mathrm{2}} \\ $$$${for}\:{which}\:\langle{u}_{\mathrm{1}} ,{w}_{\mathrm{2}} \rangle\:=\:\mathrm{0}\:{and}\:\langle{u}_{\mathrm{2}} ,{w}_{\mathrm{2}} \rangle\:=\mathrm{0} \\ $$$$\Rightarrow\langle{u}_{\mathrm{1}} ,{w}_{\mathrm{2}} \rangle\:=\:\frac{{x}}{\mathrm{3}}+\frac{\mathrm{2}{y}}{\mathrm{3}}+\frac{\mathrm{2}{z}}{\mathrm{3}}\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\langle{u}_{\mathrm{2}} ,{w}_{\mathrm{2}} \rangle\:=\:\frac{{y}}{\:\sqrt{\mathrm{2}}}\:−\frac{{z}}{\:\sqrt{\mathrm{2}}}\:=\:\mathrm{0} \\ $$$${set}\:{z}=−\mathrm{1}\:{and}\:{find}\:{the}\:{solution}\: \\ $$$${w}_{\mathrm{2}} \:=\:\left(\mathrm{4},−\mathrm{1},−\mathrm{1}\right)\:.\:{Normalize}\:{w}_{\mathrm{2}} \\ $$$${and}\:{obtain}\:{the}\:{third}\:{row}\:{of}\:{A}\:,\:{that}\:{is} \\ $$$${u}_{\mathrm{3}} \:=\:\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{18}}},\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{18}}},\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{18}}}\right)\: \\ $$$${Thus}\:{A}\:=\:\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}}\\{\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:}\\{\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{18}}}\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{18}}}\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{18}}}}\end{pmatrix}\: \\ $$$${We}\:{emphasize}\:{that}\:{the}\:{above}\:{matrix}\:{A} \\ $$$${is}\:{not}\:{unique}. \\ $$
Commented by bemath last updated on 06/Oct/20
$$\mathrm{waw}...\:\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{mr}\:\mathrm{farmer}\:\mathrm{math} \\ $$
