Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116557 by Bird last updated on 04/Oct/20

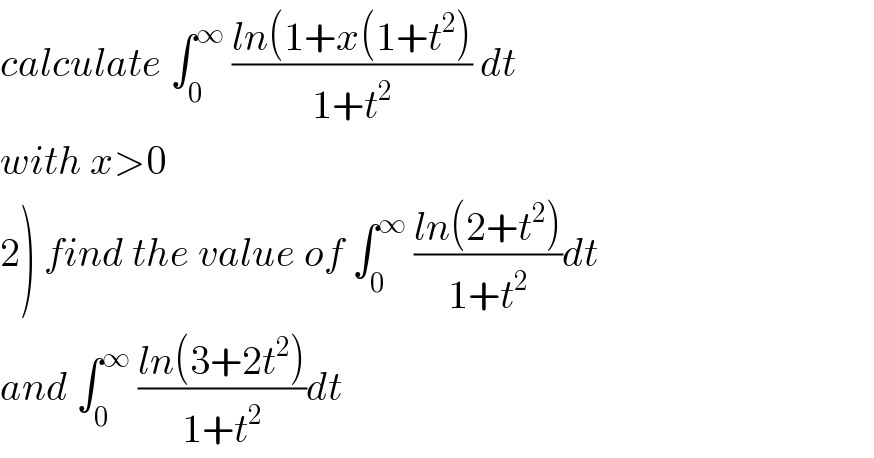
calculate ∫_0 ^∞ ((ln(1+x(1+t^2 ))/(1+t^2 )) dt with x>0 2) find the value of ∫_0 ^∞ ((ln(2+t^2 ))/(1+t^2 ))dt and ∫_0 ^∞ ((ln(3+2t^2 ))/(1+t^2 ))dt

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{1}+{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right.}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$ $${with}\:{x}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{2}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$ $${and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{3}+\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$

Answered by mindispower last updated on 05/Oct/20

f(x)=∫_0 ^∞ ((ln(1+x(1+t^2 )))/(1+t^2 ))dt f′(x)=∫_0 ^∞ (dt/(1+x(1+t^2 ))) =∫_0 ^∞ (dt/((1+x)(1+((t/( (√(1+x)))))^2 ))) =(1/( (√(1+x))))[tan^(−1) ((t/( (√(1+x)))))]_0 ^∞ =(π/(2(√(1+x)))) f(0)=0 f(x)=∫_0 ^x (π/(2(√(1+x))))=π(√(1+x)) ∫_0 ^∞ ((ln(2+t^2 ))/(1+t^2 ))dt=f(1)=π(√2) ∫_0 ^∞ ((ln(3+2t^2 ))/(1+t^2 ))dt=f(2)=π(√3)

$${f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$ $${f}'\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\left(\frac{{t}}{\:\sqrt{\mathrm{1}+{x}}}\right)^{\mathrm{2}} \right)} \\ $$ $$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\mathrm{1}+{x}}}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$ $$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\: \\ $$ $${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$ $${f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{\pi}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}=\pi\sqrt{\mathrm{1}+{x}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{2}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={f}\left(\mathrm{1}\right)=\pi\sqrt{\mathrm{2}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{3}+\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={f}\left(\mathrm{2}\right)=\pi\sqrt{\mathrm{3}} \\ $$ $$ \\ $$

Commented bymathmax by abdo last updated on 05/Oct/20

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented bymathmax by abdo last updated on 05/Oct/20

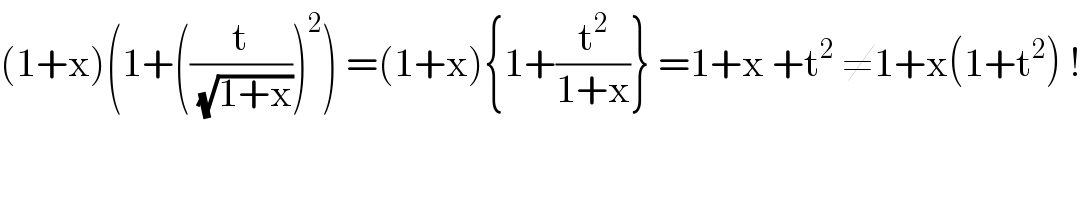
(1+x)(1+((t/(√(1+x))))^2 ) =(1+x){1+(t^2 /(1+x))} =1+x +t^2 ≠1+x(1+t^2 ) !

$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\left(\frac{\mathrm{t}}{\sqrt{\mathrm{1}+\mathrm{x}}}\right)^{\mathrm{2}} \right)\:=\left(\mathrm{1}+\mathrm{x}\right)\left\{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}}\right\}\:=\mathrm{1}+\mathrm{x}\:+\mathrm{t}^{\mathrm{2}} \:\neq\mathrm{1}+\mathrm{x}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\:! \\ $$ $$ \\ $$

Answered by mathmax by abdo last updated on 05/Oct/20

1) let f(x)=∫_0 ^∞ ((ln(1+x(1+t^2 )))/(1+t^2 ))dt we have f^′ (x)=∫_0 ^∞ (dt/(1+x(1+t^2 ))) =∫_0 ^∞ (dt/(xt^2 +x+1)) =(1/x) ∫_0 ^∞ (dt/(t^2 +((x+1)/x))) =_(t=(√((x+1)/x))u) (1/x).(x/(x+1))∫_0 ^∞ (1/(u^2 +1))((√(x+1))/(√x))du =(1/((√x)(√(x+1)))) ⇒ f(x) =∫ (dx/((√x)(√(x+1)))) +c =_((√x)=z) ∫ ((2zdz)/(z(√(z^2 +1)))) +c =2 ∫ (dz/(√(z^2 +1))) +c =2ln(z+(√(1+z^2 ))) +c =2ln((√x)+(√(1+x))) +c f(0)=0 =2ln(1)+c =c ⇒f(x) =2ln((√x)+(√(1+x))) 2)∫_0 ^∞ ((ln(2+t^2 ))/(1+t^2 ))dt =f(1) =2ln(1+(√2)) ∫_0 ^∞ ((ln(3+2t^2 ))/(1+t^2 ))dt =f(2) =2ln((√2)+(√3))

$$\left.\mathrm{1}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{x}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{xt}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}\:=_{\mathrm{t}=\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}\mathrm{u}} \:\:\frac{\mathrm{1}}{\mathrm{x}}.\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\frac{\sqrt{\mathrm{x}+\mathrm{1}}}{\sqrt{\mathrm{x}}}\mathrm{du} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{x}}\sqrt{\mathrm{x}+\mathrm{1}}}\:\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)\:=\int\:\frac{\mathrm{dx}}{\sqrt{\mathrm{x}}\sqrt{\mathrm{x}+\mathrm{1}}}\:+\mathrm{c} \\ $$ $$=_{\sqrt{\mathrm{x}}=\mathrm{z}} \:\:\:\int\:\frac{\mathrm{2zdz}}{\mathrm{z}\sqrt{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}}\:+\mathrm{c}\:=\mathrm{2}\:\int\:\frac{\mathrm{dz}}{\sqrt{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}}\:+\mathrm{c} \\ $$ $$=\mathrm{2ln}\left(\mathrm{z}+\sqrt{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\right)\:+\mathrm{c}\:=\mathrm{2ln}\left(\sqrt{\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{x}}\right)\:+\mathrm{c} \\ $$ $$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:=\mathrm{2ln}\left(\mathrm{1}\right)+\mathrm{c}\:=\mathrm{c}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{2ln}\left(\sqrt{\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{x}}\right) \\ $$ $$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{f}\left(\mathrm{1}\right)\:=\mathrm{2ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{3}+\mathrm{2t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{f}\left(\mathrm{2}\right)\:=\mathrm{2ln}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com