
Question Number 116516 by sandy_delta last updated on 04/Oct/20
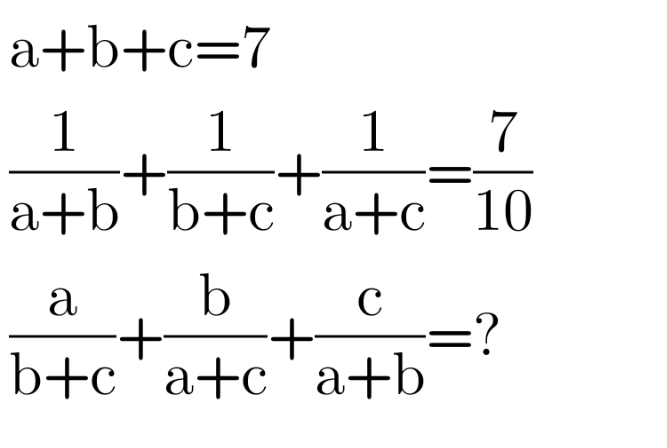
Answered by som(math1967) last updated on 04/Oct/20
![((1/(a+b))+(1/(b+c))+(1/(c+a)))(a+b+c)=(a+b+c)×(7/(10)) ((a+b+c)/(a+b))+((a+b+c)/(b+c))+((a+b+c)/(c+a))=((49)/(10)) [∵a+b+c=7] 1+(c/(a+b))+1+(a/(b+c))+1+(b/(a+c))=((49)/(10)) ∴(a/(b+c))+(b/(a+c))+(c/(a+b))=((49)/(10))−3=((19)/(10))ans](Q116518.png)
$$\left(\frac{\mathrm{1}}{\mathrm{a}+\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{b}+\mathrm{c}}+\frac{\mathrm{1}}{\mathrm{c}+\mathrm{a}}\right)\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)=\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)×\frac{\mathrm{7}}{\mathrm{10}} \\ $$$$\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{a}+\mathrm{b}}+\frac{\mathrm{a}+\mathrm{b}+{c}}{\mathrm{b}+\mathrm{c}}+\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{c}+\mathrm{a}}=\frac{\mathrm{49}}{\mathrm{10}} \\ $$$$\left[\because\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{7}\right] \\ $$$$\mathrm{1}+\frac{\mathrm{c}}{\mathrm{a}+\mathrm{b}}+\mathrm{1}+\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}+\mathrm{1}+\frac{\mathrm{b}}{\mathrm{a}+\mathrm{c}}=\frac{\mathrm{49}}{\mathrm{10}} \\ $$$$\therefore\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}+\frac{\mathrm{b}}{\mathrm{a}+\mathrm{c}}+\frac{\mathrm{c}}{\mathrm{a}+\mathrm{b}}=\frac{\mathrm{49}}{\mathrm{10}}−\mathrm{3}=\frac{\mathrm{19}}{\mathrm{10}}\mathrm{ans} \\ $$
Commented by sandy_delta last updated on 04/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Answered by bobhans last updated on 05/Oct/20
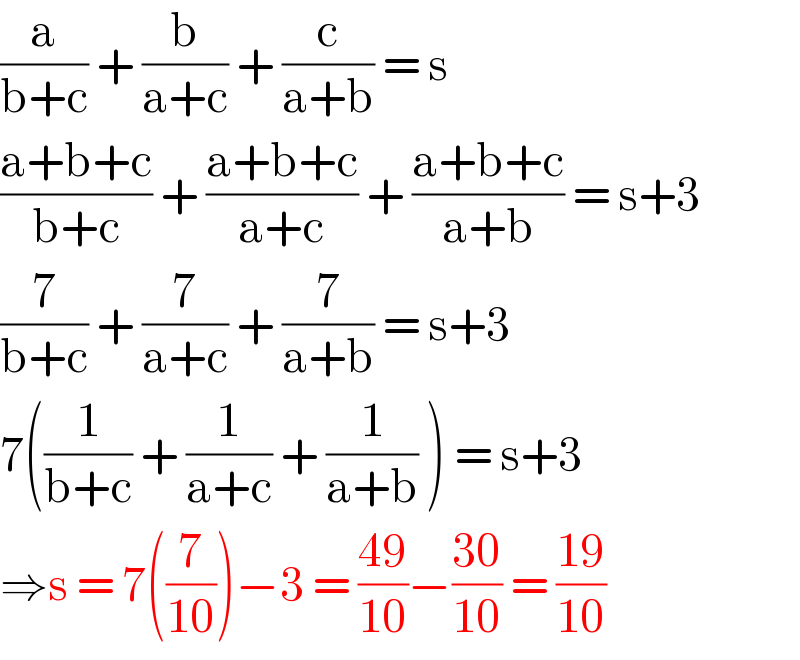
$$\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}\:+\:\frac{\mathrm{b}}{\mathrm{a}+\mathrm{c}}\:+\:\frac{\mathrm{c}}{\mathrm{a}+\mathrm{b}}\:=\:\mathrm{s}\: \\ $$$$\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{b}+\mathrm{c}}\:+\:\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{a}+\mathrm{c}}\:+\:\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{a}+\mathrm{b}}\:=\:\mathrm{s}+\mathrm{3} \\ $$$$\frac{\mathrm{7}}{\mathrm{b}+\mathrm{c}}\:+\:\frac{\mathrm{7}}{\mathrm{a}+\mathrm{c}}\:+\:\frac{\mathrm{7}}{\mathrm{a}+\mathrm{b}}\:=\:\mathrm{s}+\mathrm{3}\: \\ $$$$\mathrm{7}\left(\frac{\mathrm{1}}{\mathrm{b}+\mathrm{c}}\:+\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{c}}\:+\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{b}}\:\right)\:=\:\mathrm{s}+\mathrm{3}\: \\ $$$$\Rightarrow\mathrm{s}\:=\:\mathrm{7}\left(\frac{\mathrm{7}}{\mathrm{10}}\right)−\mathrm{3}\:=\:\frac{\mathrm{49}}{\mathrm{10}}−\frac{\mathrm{30}}{\mathrm{10}}\:=\:\frac{\mathrm{19}}{\mathrm{10}} \\ $$
