
Question Number 116331 by bobhans last updated on 03/Oct/20
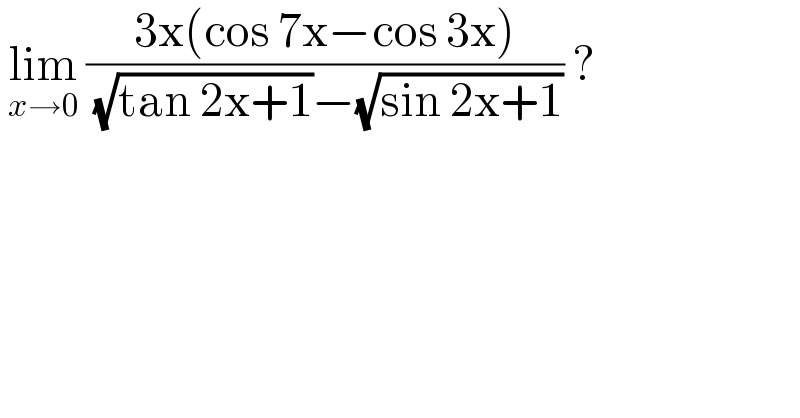
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3x}\left(\mathrm{cos}\:\mathrm{7x}−\mathrm{cos}\:\mathrm{3x}\right)}{\:\sqrt{\mathrm{tan}\:\mathrm{2x}+\mathrm{1}}−\sqrt{\mathrm{sin}\:\mathrm{2x}+\mathrm{1}}}\:? \\ $$
Answered by bemath last updated on 03/Oct/20
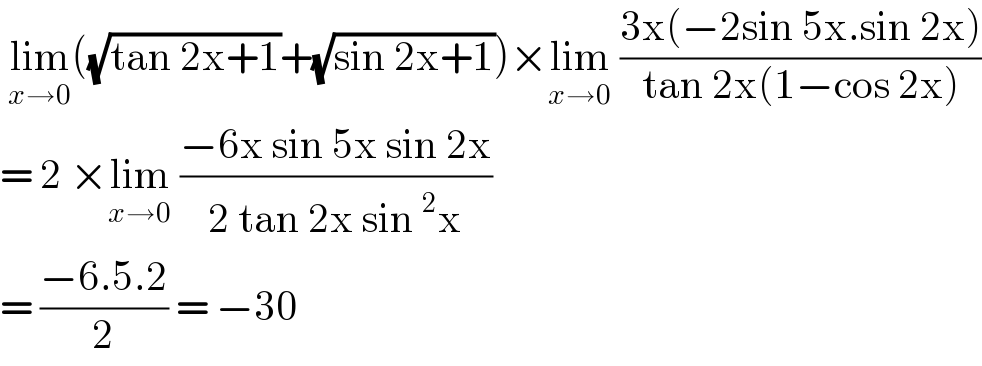
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\sqrt{\mathrm{tan}\:\mathrm{2x}+\mathrm{1}}+\sqrt{\mathrm{sin}\:\mathrm{2x}+\mathrm{1}}\right)×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3x}\left(−\mathrm{2sin}\:\mathrm{5x}.\mathrm{sin}\:\mathrm{2x}\right)}{\mathrm{tan}\:\mathrm{2x}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2x}\right)} \\ $$$$=\:\mathrm{2}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{6x}\:\mathrm{sin}\:\mathrm{5x}\:\mathrm{sin}\:\mathrm{2x}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{2x}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$=\:\frac{−\mathrm{6}.\mathrm{5}.\mathrm{2}}{\mathrm{2}}\:=\:−\mathrm{30} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Oct/20
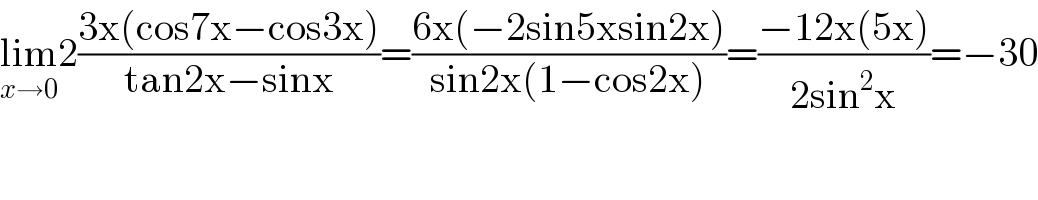
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}2}\frac{\mathrm{3x}\left(\mathrm{cos7x}−\mathrm{cos3x}\right)}{\mathrm{tan2x}−\mathrm{sinx}}=\frac{\mathrm{6x}\left(−\mathrm{2sin5xsin2x}\right)}{\mathrm{sin2x}\left(\mathrm{1}−\mathrm{cos2x}\right)}=\frac{−\mathrm{12x}\left(\mathrm{5x}\right)}{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}}=−\mathrm{30} \\ $$
