
Question Number 116323 by bobhans last updated on 03/Oct/20
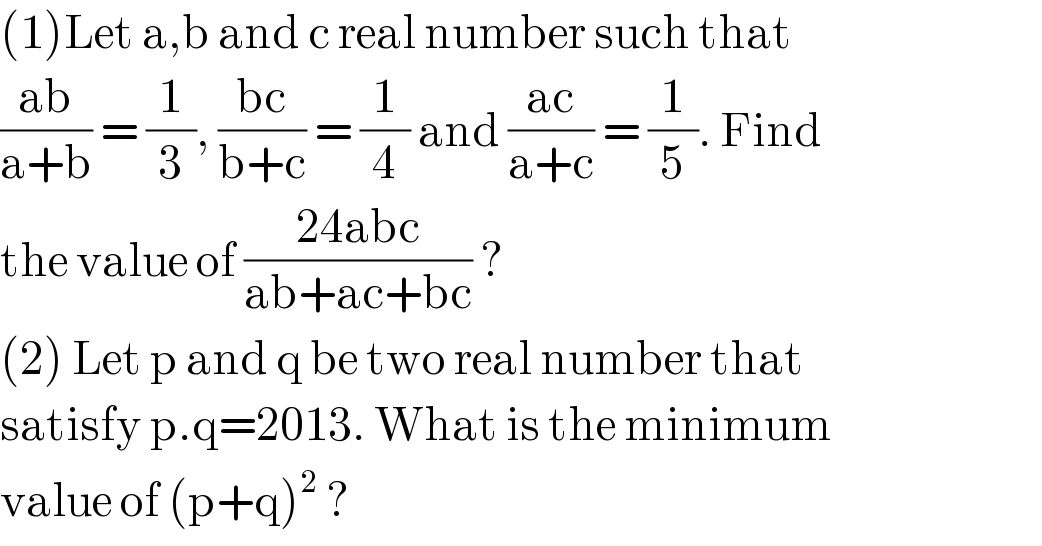
$$\left(\mathrm{1}\right)\mathrm{Let}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{real}\:\mathrm{number}\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}\:=\:\frac{\mathrm{1}}{\mathrm{3}},\:\frac{\mathrm{bc}}{\mathrm{b}+\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{and}\:\frac{\mathrm{ac}}{\mathrm{a}+\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{5}}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{24abc}}{\mathrm{ab}+\mathrm{ac}+\mathrm{bc}}\:? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Let}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{be}\:\mathrm{two}\:\mathrm{real}\:\mathrm{number}\:\mathrm{that} \\ $$$$\mathrm{satisfy}\:\mathrm{p}.\mathrm{q}=\mathrm{2013}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} \:? \\ $$
Answered by john santu last updated on 03/Oct/20

$$\left(\mathrm{1}\right)\:\rightarrow\begin{cases}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\mathrm{3}}\\{\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\mathrm{4}\:}\\{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{c}}=\mathrm{5}}\end{cases} \\ $$$$\:\:\:\:\:{summing}\:{the}\:{three}\:{equation} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\:=\:\mathrm{12}\: \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\:=\:\mathrm{6}\:;\:\frac{{ab}+{ac}+{bc}}{{abc}}\:=\:\mathrm{6} \\ $$$$\Rightarrow\:\frac{{abc}}{{ab}+{ac}+{bc}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:,\:{multiply}\:{both} \\ $$$${sides}\:{by}\:\mathrm{24}\:{we}\:{get}\:\frac{\mathrm{24}{abc}}{{ab}+{ac}+{bc}}\:=\:\mathrm{4} \\ $$$$ \\ $$
Answered by john santu last updated on 03/Oct/20
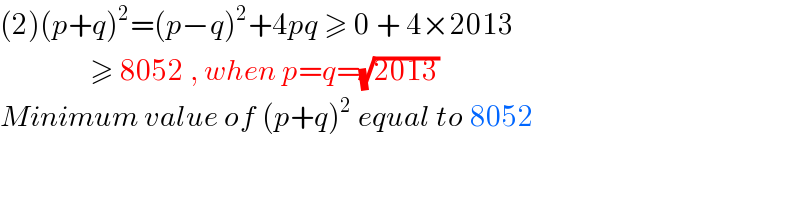
$$\left(\mathrm{2}\right)\left({p}+{q}\right)^{\mathrm{2}} =\left({p}−{q}\right)^{\mathrm{2}} +\mathrm{4}{pq}\:\geqslant\:\mathrm{0}\:+\:\mathrm{4}×\mathrm{2013} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant\:\mathrm{8052}\:,\:{when}\:{p}={q}=\sqrt{\mathrm{2013}} \\ $$$${Minimum}\:{value}\:{of}\:\left({p}+{q}\right)^{\mathrm{2}} \:{equal}\:{to}\:\mathrm{8052} \\ $$
