
Question Number 116094 by Engr_Jidda last updated on 30/Sep/20
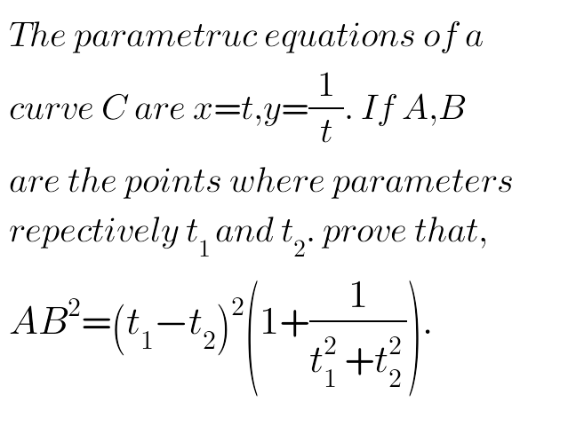
Answered by 1549442205PVT last updated on 01/Oct/20

$$\mathrm{A}\left(\mathrm{t}_{\mathrm{1}} ,\frac{\mathrm{1}}{\mathrm{t}_{\mathrm{1}} }\right),\mathrm{B}\left(\mathrm{t}_{\mathrm{2}} ,\frac{\mathrm{1}}{\mathrm{t}_{\mathrm{2}} }\right)\Rightarrow\overset{\rightarrow} {\mathrm{AB}}=\left(\mathrm{t}_{\mathrm{2}} −\mathrm{t}_{\mathrm{1}} ,\frac{\mathrm{1}}{\mathrm{t}_{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}_{\mathrm{1}} }\right) \\ $$$$\Rightarrow\mathrm{AB}^{\mathrm{2}} =\left(\mathrm{t}_{\mathrm{2}} −\mathrm{t}_{\mathrm{1}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{t}_{\mathrm{1}} −\mathrm{t}_{\mathrm{2}} }{\mathrm{t}_{\mathrm{1}} \mathrm{t}_{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{t}_{\mathrm{1}} −\mathrm{t}_{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{t}_{\mathrm{2}} ^{\mathrm{2}} }\right) \\ $$$$\boldsymbol{\mathrm{It}}\:\boldsymbol{\mathrm{seems}}\:\boldsymbol{\mathrm{question}}\:\boldsymbol{\mathrm{giving}}\:\boldsymbol{\mathrm{false}}\:\boldsymbol{\mathrm{conclusion}} \\ $$
