
Question Number 116085 by Ar Brandon last updated on 30/Sep/20
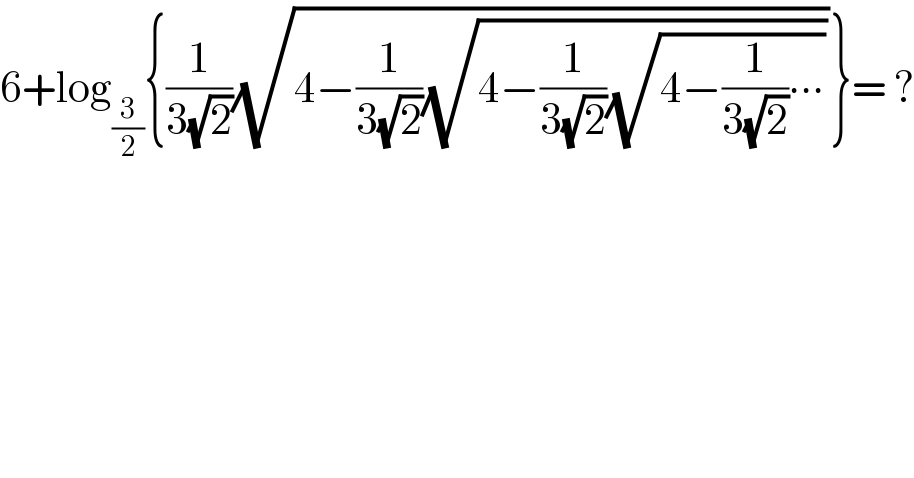
$$\mathrm{6}+\mathrm{log}_{\frac{\mathrm{3}}{\mathrm{2}}} \left\{\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\centerdot\centerdot\centerdot}}}\right\}=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 30/Sep/20
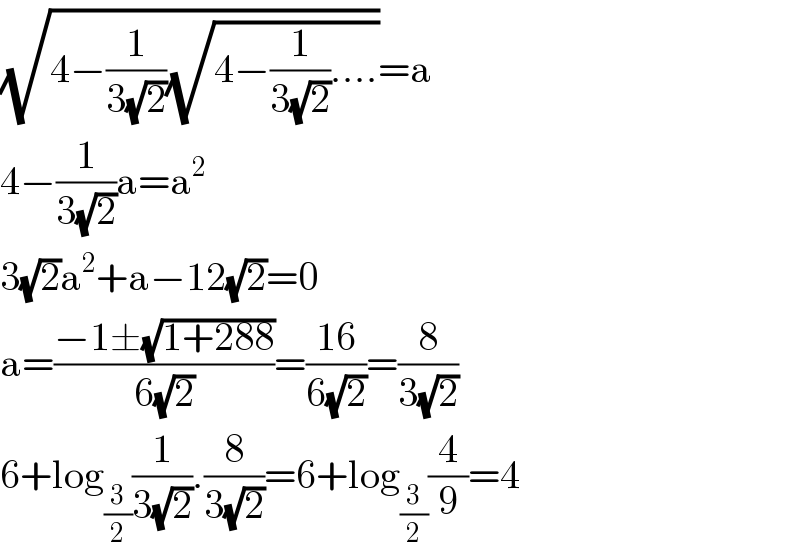
$$\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}....}}=\mathrm{a} \\ $$$$\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\mathrm{a}=\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{3}\sqrt{\mathrm{2}}\mathrm{a}^{\mathrm{2}} +\mathrm{a}−\mathrm{12}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{a}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{288}}}{\mathrm{6}\sqrt{\mathrm{2}}}=\frac{\mathrm{16}}{\mathrm{6}\sqrt{\mathrm{2}}}=\frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{6}+\mathrm{log}_{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}.\frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{2}}}=\mathrm{6}+\mathrm{log}_{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{4}}{\mathrm{9}}=\mathrm{4} \\ $$
